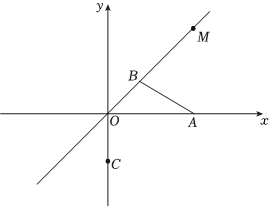
如图，在平面直角坐标系中，已知：OM是过原点的一条直线，点B是OM上一点，点B的坐标为（2，2），点A是x轴上一点，且∠AOM=45°，S△AOB=5．点C是y轴负半轴一点，OC：OA=3：5．
（1）求点A的坐标．
（2）点N是直线OM上的一个动点，当AN+CN的值最小时，请直接写出AN+CN的最小值．
（3）在y轴上是否存在点D，使以点B，O，D为顶点的三角形为等腰三角形？若存在，请直接写出满足条件的点D的个数，并试着直接写出两个满足条件的点D的坐标；若不存在，说明理由．
【考点】三角形综合题．
【答案】（1）（5，0）；
（2）8；
（3）点D有四个，其坐标为（0，-2）或（0，2）或（0，2）或（0，4）．
（2）8；
（3）点D有四个，其坐标为（0，-2
2
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/29 21:0:2组卷：25引用：1难度：0.4
相似题
-
1．【问题探究】在学习三角形中线时，我们遇到过这样的问题：如图①，在△ABC中，点D为BC边上的中点，AB=4，AC=6，求线段AD长的取值范围．我们采用的方法是延长线段AD到点E，使得AD=DE，连结CE，可证△ABD≌△ECD，可得CE=AB=4，根据三角形三边关系可求AD的范围，我们将这样的方法称为“三角形倍长中线”．则AD的范围是：．
【拓展应用】
（1）如图②，在△ABC中，BC=2BD，AD=3，AC=2，∠BAD=90°，求AB的长．10
（2）如图③，在△ABC中，D为BC边的中点，分别以AB、AC为直角边向外作直角三角形，且满足∠ABE=∠ACF=30°，连结EF，若AD=2，则EF=．（直接写出）3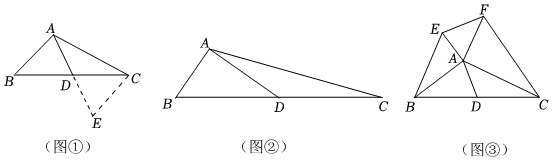
发布：2025/5/26 8:0:5组卷：411引用：5难度：0.4 -
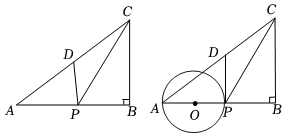2．如图①，在△ABC中，∠ABC=90°，AC=10，BC=6，D点为AC边的中点．点P在边AB上运动（点P不与A、B重合），连结PD、PC．设线段AP的长度为x.
（1）求AB的长．
（2）当△APD是等腰三角形时，求这个等腰三角形的腰长．
（3）连结PD、PC，当PD+PC取最小值时，求x的值．
（4）如图②，取AP的中点为O，以点O为圆心，以线段AP的长为直径的圆与线段PD有且只有一个公共点时，直接写出x的取值范围．发布：2025/5/26 6:30:2组卷：176引用：1难度：0.3 -
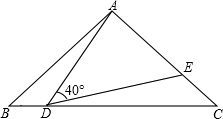3．如图，在△ABC中，AB=AC=2，∠B=40°，点D在线段BC上运动（D不与B、C重合），连接AD，作∠ADE=40°，DE交线段AC于E．
（1）当∠BDA=115°时，∠BAD=°，∠DEC=°；
（2）当DC等于多少时，△ABD与△DCE全等？请说明理由；
（3）在点D的运动过程中，△ADE的形状可以是等腰三角形吗？若可以，请直接写出∠BDA的度数．若不可以，请说明理由．发布：2025/5/26 2:30:2组卷：976引用：8难度：0.3
