下面是小明设计“作三角形一边上的高”的尺规作图和证明过程．
已知：△ABC中，∠BAC=90°，求作：△ABC的边BC上的高AD．
作法：（1）分别以点B和点C为圆心．BA、CA为半径作弧，两弧相交于点E．
（2）作直线AE交BC边于点D．
所以线段AD就是所求作的高．
证明：连接BE，CF，
∵BA=BE，
∴点B在线段AE的垂直分线上（依据：____）．
同理可证，点C也在线段，AE的垂直平分线上，
∴BC垂直平分AE，
∴AD是△ABC的高．
（1）根据小明设计的尺规作图过程，使用直尺和圆规．补全图形（保留作图痕迹）；
（2）小明证明过程中的依据是：到线段两端距离相等的点在线段的垂直平分线上到线段两端距离相等的点在线段的垂直平分线上；
（3）善于思考的小明提出了这样一个问题，若CD=2cm,∠ACB=60°，BC的长度又是多少呢？请你帮助小明完成解答过程．
【答案】到线段两端距离相等的点在线段的垂直平分线上
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/20 7:0:2组卷：33引用：4难度：0.5
相似题
-
1．用直尺和圆规作线段的垂直平分线，下列作法正确的是（ ）
发布：2025/6/15 15:30:1组卷：242引用：4难度：0.9 -
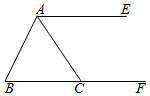2．如图，AE∥BF，AC平分∠BAE，交BF于C．
（1）尺规作图：过点B作AC的垂线，交AC于O，交AE于D，（保留作图痕迹，不写作法）；
（2）求证：AD=BC．发布：2025/6/15 19:0:1组卷：346引用：2难度：0.5 -
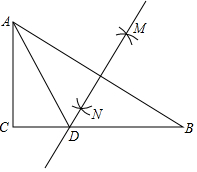3．如图，在Rt△ABC中，∠C=90°，AB＞BC，分别以顶点A，B为圆心，以大于AB长为半径作圆弧，两条圆弧交于点M，N，作直线MN交边CB于点D．若AD=5，CD=3，则BC的长是 ．12发布：2025/6/15 17:0:2组卷：12引用：1难度：0.7
