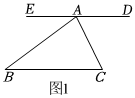
如图1,已知点A是BC外一点,连接AB,AC.求∠BAC+∠B+∠C的度数.
(1)阅读并补充下面推理过程:
解:过点A作ED∥BC,
所以∠B=∠EAB∠EAB,∠C=∠DAC∠DAC.
又因为∠EAB+∠BAC+∠DAC=180°,
所以∠B+∠BAC+∠C=180°.
(2)从上面的推理过程中,我们发现平行线具有“等角转化”的功能,将∠BAC,∠B,∠C“凑”在一起,得出角之间的关系,使问题得以解决.
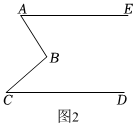
如图2,已知AE∥CD,试说明∠ABC=∠A+∠C.
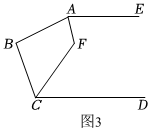
(3)如图3,已知AE∥CD,AF平分∠BAE,CF平分∠BCD,若∠ABC=100°,则∠AFC的度数为 130130°;
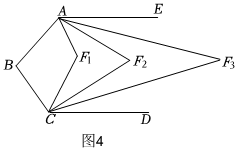
(4)如图4,已知AE∥CD,AF1平分∠BAE,CF1平分∠BCD,AF2平分∠EAF1,CF2平分∠DCF1,AF3平分∠EAF2,CF3平分∠DCF2…,若∠ABC=a°,则∠Fn的度数为 12n(360°-a°)12n(360°-a°);(用含a的代数式表示)
1
2
n
(
360
°
-
a
°
)
1
2
n
(
360
°
-
a
°
)
【答案】∠EAB;∠DAC;130;
1
2
n
(
360
°
-
a
°
)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/31 8:0:9组卷:349引用:1难度:0.3
相似题
-
 1.如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )发布:2025/5/23 21:30:2组卷:106引用:5难度:0.8
1.如图,AB∥CD,∠1=30°,∠2=40°,则∠3的度数为( )发布:2025/5/23 21:30:2组卷:106引用:5难度:0.8 -
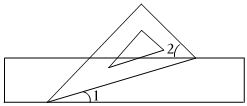 2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边可以自由滑动上.当∠1=15°时,∠2的度数是( )发布:2025/5/23 22:0:2组卷:359引用:3难度:0.6
2.如图,有一块含有30°角的直角三角板的两个顶点放在直尺的对边可以自由滑动上.当∠1=15°时,∠2的度数是( )发布:2025/5/23 22:0:2组卷:359引用:3难度:0.6 -
 3.如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为( )发布:2025/5/23 22:30:2组卷:1924引用:4难度:0.8
3.如图,是一张长方形纸片(其中AB∥CD),点E,F分别在边AB,AD上.把这张长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH=4∠AEF,则∠CHG的度数为( )发布:2025/5/23 22:30:2组卷:1924引用:4难度:0.8


