请仔细观察图中有关辅助线的画法,从中任选一个,证明多边形内角和定理:n边形的内角和等于(n-2)•180,下面已给出已知、求证,请把你选择的方法及证明多边形内角和定理的过程写出来.
方法一:在n边形A1 A2 A3 A4 A5…An中任取一点O,连接O与各个顶点.
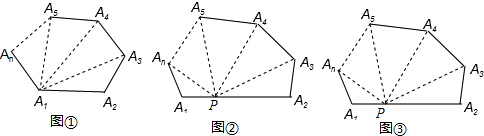
方法二:作过顶点A的所有对角线.
方法三:在n边形的边A1A2上任取一点P,连接这点与各个顶点.
已知:n边形A1 A2 A3 A4 A5…An,求证:n边形A1 A2 A3 A4 A5…An的内角和等于(n-2)•180°.
【答案】见试题解答内容
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/7/28 8:0:9组卷:62引用:2难度:0.9


