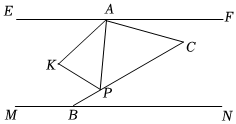
如图，直线EF∥MN，点A、B分别在直线EF、MN上，点C在EF和MN之间，且满足∠CBN=2∠FAC，∠CAF＜30°，点P为线段BC上一点（端点除外），∠EAP的平分线与∠BPA的平分线交于点K．
（1）当∠ACB=45°时，求∠CBN；
（2）请用等式表示∠AKP与∠CAF的数量关系；
（3）若2∠AKP-∠PAF=90°时，判断线段AP与AC的大小关系，并说明理由．
【答案】（1）30°；
（2）∠AKP=90°-∠CAF．（或∠AKP+∠CAF=90°），理由见解答；
（3）AP＜AC．理由见解答．
（2）∠AKP=90°-∠CAF．（或∠AKP+∠CAF=90°），理由见解答；
（3）AP＜AC．理由见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/8 8:0:9组卷：405引用：1难度：0.3
