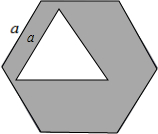
小明用边长为3厘米的木条做了个正三角形框架，之后又用半径为1厘米的圆沿着这个架子的外围滚了一圈．
（1）求这个圆扫过的面积是

（18+4π）cm²

（18+4π）cm²

；
（2）小明又用同样长度的木条做了个正五边形（五条边相等，五个内角相等的图形）的框架，那么再用半径为1厘米的圆沿着这个架子的外围滚了一圈其扫过的面积又是

（30+4π）cm²

（30+4π）cm²

；
（3）当用同样长度的木条做正n边形（n条边相等，n个内角相等的图形）的框架，再用半径为1厘米的圆沿着这个架子的外围滚一圈．圆扫过的图形都是由扇形和长方形组成，现标记这个扇形的圆心角大小为β°，正n边形的内角大小为α°，请写出α与β之间的数量关系

α+β=180°

α+β=180°

，并用含n的式子表示α的大小，则α=

（

n

-

2

）

×

180

°

n

（

n

-

2

）

×

180

°

n

．