百合外国语学校着力培养学生的数学探究能力．在数学综合实践活动课上，钱三一同学借助于两根小木棒m、n研究数学问题：
如图，他把两根木棒放在数轴上，木棒的端点A、B、C、D在数轴上对应的数分别为a、b、c、d,已知|a+5|+（b+1）2=0，c=3，d=8．
（1）a=-5-5，b=-1-1．
（2）钱三一同学把木棒m、n同时沿x轴正方向移动，m、n的速度分别为4个单位/s和3个单位/s,设平移时间为t（s）．
①若在平移过程中原点O恰好是木棒m的中点，则t=3434（s）；
②在平移过程中，当木棒m、n重叠部分的长为2个单位长度时，求t的值．
3
4
3
4
【考点】几何变换综合题．
【答案】-5；-1；
3
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/14 8:0:9组卷：863引用：1难度：0.7
相似题
-
1．阅读下面的材料，并解决问题：
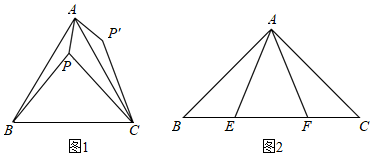
（1）如图1，等边△ABC内有一点P，若点P到顶点A、B、C的距离分别是3、4、5，求∠APB的度数．由于PA、PB、PC不在一个三角形中，为了解决本题我们可以将△ABP绕顶点A旋转到△ACP′处，此时△ACP≌．这样，就可以利用全等三角形知识，将三条线段的长度转化到一个三角形中从而求出∠APB的度数；（求∠APB的度数）
（2）请你利用第（1）题解答的思想方法，解答下面的问题：如图2，在△ABC中，∠CAB=90°，AB=AC，E、F为BC上的点且∠EAF=45°，求证：EF2=BE2+FC2．发布：2025/6/9 5:30:2组卷：189引用：2难度：0.2 -
2．如图1，在△ABC中，AE⊥BC于点E，AE=BE，D是AE上的一点，且DE=CE，连接BD，CD．
（1）试判断BD与AC的位置关系是：；数量关系是：；
（2）如图2，若将△DCE绕点E旋转一定的角度后，试判断BD与AC的位置关系和数量关系是否发生变化，并说明理由；
（3）如图3，若将（2）中的等腰直角三角形都换成等边三角形，其他条件不变．
①试猜想BD与AC的数量关系为：；
②你能求出BD与AC的夹角度数吗？如果能，请直接写出夹角度数；如果不能，请说明理由．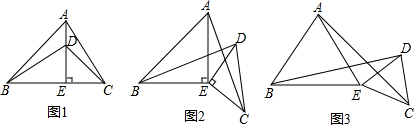
发布：2025/6/9 6:30:1组卷：724引用：2难度：0.3 -
3．在Rt△ABC中，∠ACB=90°，AC=3，BC=4．将Rt△ABC绕点B顺时针旋转α（0°＜α＜60°）得到Rt△DEB，直线DE，AC交于点P．
（1）如图1，当BD⊥BC时，连接BP．
①求△BDP的面积；
②求tan∠CBP的值；
（2）如图2，连接AD，若F为AD中点，求证：C，E，F三点共线．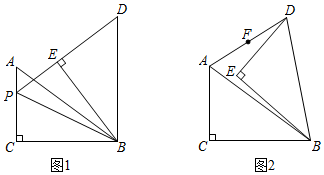
发布：2025/6/9 17:0:1组卷：511引用：4难度：0.1
