综合与实践：【问题情境】：通过查看出厂包装袋上的数据，数学活动小组的同学发现A4纸的长与宽分别为297mm和210mm,其比值为297210≈1.414，而2≈1.414，他们上网查阅资料也发现A4纸的长与宽的比是一个特殊值“2”．不妨定义长与宽的比为2：1的矩形为“标准矩形”．【操作实践】：如图1，数学活动小组的同学在几何画板软件上画了一个正方形ABCD，连接对角线BD，在射线DC上截取了DE=DB，过点E作EF⊥AB交AB的延长线于点F，令AB=1．
【问题探究】：（1）求证：四边形AFED为“标准矩形”；
（2）如图2，数学活动小组的同学在图1的基础上隐藏了线段BC，在线段EF上取一点P，连接BP，DP．
①当DP平分∠BDE时，求PF的长；
②当△BDP的周长最小时，求∠PBF的正切值．
297
210
≈
1
.
414
2
≈
1
.
414
2
2
：
1
【考点】四边形综合题．
【答案】（1）证明见解答过程；
（2）①；
②．
（2）①
PF
=
2
-
1
②
2
2
+
1
7
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/11 8:0:9组卷：313引用：7难度：0.1
相似题
-
1．如图1，四边形ABCD是矩形，点P是对角线AC上的一个动点（不与A、C重合），过点P作PE⊥CD于点E，连接PB，已知AD=3，AB=4，设AP=m.
（1）当m=1时，求PE的长；
（2）连接BE，试问点P在运动的过程中，能否使得△PAB≌△PEB？请说明理由；
（3）如图2，过点P作PF⊥PB交CD边于点F，设CF=n,试判断5m+4n的值是否发生变化，若不变，请求出它的值；若变化，请说明理由．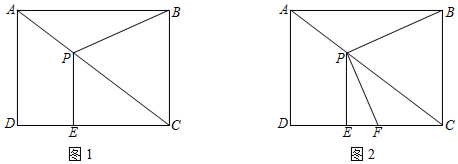
发布：2025/6/17 0:0:1组卷：783引用：4难度：0.2 -
2．（1）如图①，把三角形纸片ABC沿DE折叠，当点A落在四边形BCED的内部时，若∠B=50°，∠C=85°，求∠1+∠2的值；
（2）如图②，如果把△ABC纸片沿DE折叠，使点A落在四边形BCED的外部A′的位置，此时∠A与∠1、∠2之间存在什么样的等量关系？并说明理由；
（3）如果把四边形ABCD沿EF折叠，使点A、D落在四边形BCFE的内部A′、D′的位置，如图③，你能求出∠A、∠D与∠1、∠2之间的等量关系吗？（直接写出关系式即可）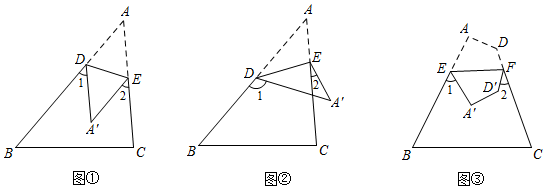
发布：2025/6/16 21:0:1组卷：229引用：2难度：0.4 -
3．（1）[问题背景]如图1，在△ABC中，AB=AC，∠BAC=α°，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转α°得到AE，连接EC，则∠BCE=°（用含α的式子表示），线段BC，DC，EC之间满足的等量关系式为；
（2）[探究证明]如图2，在Rt△ABC中，AB=AC，D为BC边上一点（不与点B、C重合）将线段AD绕点A逆时针旋转90°得到线段AE，连接DE，求证：BD2+CD2=2AD2；
（3）[拓展延伸]如图3，在四边形ABCF中，∠ABC=∠ACB=∠AFC=45°，BF=3，CF=1．将△ABF绕点A逆时针旋转90°，试画出旋转后的图形，并求出AF的长度．（不要求尺规作图）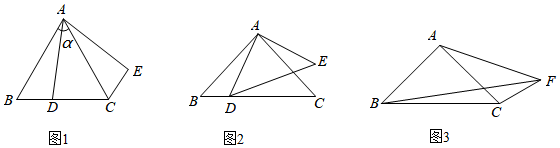
发布：2025/6/16 14:30:2组卷：1152引用：2难度：0.1
