若函数G在m≤x≤n(m<n)上的最大值记为ymax,最小值记为ymin,且满足ymax-ymin=k(k为整数),则称函数G是在m≤x≤n上的“k阶极差函数”.如函数y=x在0≤x≤1上的最大值ymax=1,最小值ymin=0,因此ymax-ymin=1,则称函数y=x是在0≤x≤1上的“1阶极差函数”,函数y=1x在14≤x≤12上的最大值ymax=4,最小值ymin=2,因此ymax-ymin=2,则称函数y=1x是在14≤x≤12上的“2阶极差函数”
(1)函数①y=1x,②y=x+1;③y=x2.其中函数 ②②是在1≤x≤4上的“3阶极差函数”;(填序号)
(2)已知函数G:y=ax2-4ax+3a(a>0).
①当a=1时,函数G是在t≤x≤t+1上的“2阶极差函数”,求t的值;
②函数G是在m+2≤x≤2m+1(m为整数)上的“3阶级差函数”,且存在整数s,使得s=ymaxymin,求a的值.
y
=
1
x
1
4
≤
x
≤
1
2
y
=
1
x
1
4
≤
x
≤
1
2
y
=
1
x
s
=
y
max
y
min
【考点】二次函数综合题.
【答案】②
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/16 6:0:3组卷:113引用:2难度:0.5
相似题
-
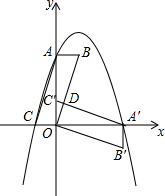 1.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.
1.如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.
(1)求A、A′、C三点的坐标;
(2)求平行四边形ABOC和平行四边形A′B′OC′重叠部分△C′OD的面积;
(3)点M是第一象限内抛物线上的一动点,问点M在何处时,△AMA′的面积最大?最大面积是多少?并写出此时M的坐标.发布:2025/6/19 9:0:1组卷:1341引用:51难度:0.5 -
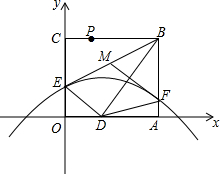 2.如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且5=ODOE,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-43x2+116x+c经过点E,且与AB边相交于点F.12
2.如图,折叠矩形OABC的一边BC,使点C落在OA边的点D处,已知折痕BE=5,且5=ODOE,以O为原点,OA所在的直线为x轴建立如图所示的平面直角坐标系,抛物线l:y=-43x2+116x+c经过点E,且与AB边相交于点F.12
(1)求证:△ABD∽△ODE;
(2)若M是BE的中点,连接MF,求证:MF⊥BD;
(3)P是线段BC上一点,点Q在抛物线l上,且始终满足PD⊥DQ,在点P运动过程中,能否使得PD=DQ?若能,求出所有符合条件的Q点坐标;若不能,请说明理由.发布:2025/6/19 9:0:1组卷:1930引用:51难度:0.5 -
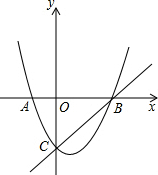 3.如图,抛物线 y=x2-12x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.32
3.如图,抛物线 y=x2-12x-2与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,M是直线BC下方的抛物线上一动点.32
(1)求A、B、C三点的坐标.
(2)连接MO、MC,并把△MOC沿CO翻折,得到四边形MO M′C,那么是否存在点M,使四边形MO M′C为菱形?若存在,求出此时点M的坐标;若不存在,说明理由.
(3)当点M运动到什么位置时,四边形ABMC的面积最大,并求出此时M点的坐标和四边形ABMC的最大面积.发布:2025/6/19 9:0:1组卷:2419引用:52难度:0.3


