探究阅读题：
【阅读】在大自然里，有很多数学的奥秘，一片美丽的心形叶片，一棵生长的幼苗都可以看作把一条抛物线的一部分沿直线折叠而形成．（如图1和图2）
【探究任务1】确定心形叶片的形状
如图3建立平面直角坐标系，心形叶片下部轮廓线可以看作是二次函数y=mx2-4mx-20m+5图象的一部分，且过原点，求抛物线的解析式和顶点D的坐标．
【探究任务2】研究心形叶片的尺寸
如图3，心形叶片的对称轴直线y=x+2与坐标轴交于A、B两点，直线x=6分别交抛物线和直线AB于点E、F点，点E、E′是叶片上的一对对称点，EE′交直线AB与点G，求叶片此处的宽度EE′．
【探究任务3】研究幼苗叶片的生长小李同学在观察幼苗生长的过程中，发现幼苗叶片下方轮廓线都可以看作是二次函数y=mx2-4mx-20m+5图象的一部分．如图4，幼苗叶片下方轮廓线正好对应探究任务1中的二次函数，已知直线PD与水平线的夹角为45°，三天后，点D长到与点P同一水平位置的点D′时，叶尖Q落在射线OP上，如图5所示，求此时幼苗叶子的长度和最大宽度．
【考点】二次函数综合题．
【答案】【探究任务1】：，顶点D的坐标为 （2，-1）；
【探究任务2】：；
【探究任务3】：叶片此时的长度为，最大宽度为．
y
=
1
4
x
2
-
x
=
1
4
（
x
-
2
）
2
-
1
【探究任务2】：
5
2
【探究任务3】：叶片此时的长度为
3
5
3
5
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/24 8:0:9组卷：750引用：2难度：0.2
相似题
-
1．如图1，在平面直角坐标系xOy中，已知抛物线y=-x2+bx+c经过A（-1，0），B（3，0）两点．P是抛物线上一点，且在直线BC的上方．
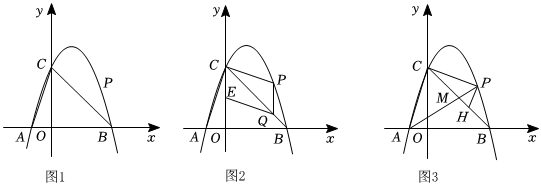
（1）求抛物线的解析式；
（2）如图2，点E为OC中点，作PQ∥y轴交BC于点Q，若四边形CPQE为平行四边形，求点P的横坐标；
（3）如图3，连结AC、AP，AP交BC于点M，作PH∥AC交BC于点H．记△PHM，△PMC，△CAM的面积分别为S1，S2，S3．判断是否存在最大值．若存在，求出最大值；若不存在，请说明理由．S1S2+S2S3发布：2025/5/23 6:0:2组卷：867引用：3难度：0.1 -
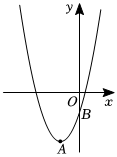2．如图，在平面直角坐标系中，抛物线y=ax2+bx-1的顶点A的坐标为，与y轴交于点B．（-34，-178）
（1）求抛物线的函数表达式；
（2）点P是抛物线上的动点，过点P作PM⊥x轴于点M，以PM为斜边作等腰直角三角形PMN，当点N恰好落在y轴上时，求点P的坐标．发布：2025/5/23 6:0:2组卷：312引用：2难度：0.3 -
3．如图1，在平面直角坐标系中，抛物线y=a（x-3）2+4过原点，与x轴的正半轴交于点A，已知B点为抛物线的顶点，抛物线的对称轴与x轴交于点D．
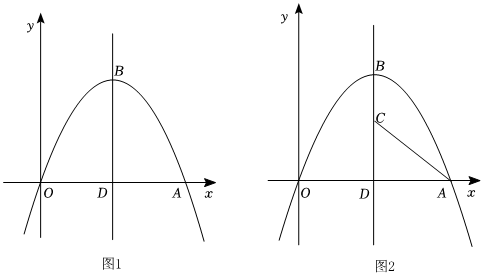
（1）求a的值，并直接写出A、B两点的坐标；
（2）若P点是该抛物线对称轴上一点，且∠BOP=45°，求点P的坐标；
（3）如图2，若C点为线段BD上一点，求3BC+5AC的最小值．发布：2025/5/23 6:0:2组卷：822引用：3难度：0.3
