（1）如图1，在△ABC中，∠A=30°，∠C=90°，求证：BC=12AB．
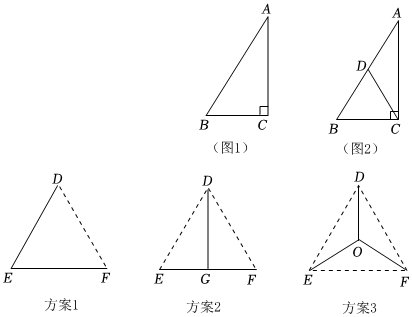
①请补全证明过程
证明：如图2．取AB中点D，连接CD．∴BD=AD=12AB．
在△ABC中，∠C=90°，∴CD=12ABCD=12AB；CD=BD．
又∠A=30°，∴∠B=90°-∠A=60°．
∴△BCD为 等边等边三角形．∴BC=BD=12AB．
②请用文字概括①所证明的命题； 在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半．
（2）如图3，某三个城镇中心D、E、F恰好分别位于一个等边三角形的三个顶点处，在三个城镇中心之间铺设通信光缆，以城镇D为出发点设计了三种连接方案：
方案1：DE+EF；
方案2：DG+EF；（以G为EF中点）；
方案3：DO+OE+OF；（以O为△DEF三边的垂直平分线的交点）．
①设DE=65，通过计算，比较三种链接方案中铺设的光缆长度的长短；
②不计算，比较三种连接方案中铺设的光缆长度的长短，并说明理由．
1
2
1
2
1
2
1
2
1
2
【考点】三角形综合题．
【答案】CD=AB；等边；在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半
1
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/25 8:0:9组卷：745引用：1难度：0.3
相似题
-
1．数学课上，李老师出示了如下的题目．
在等边三角形ABC中，点E在AB上，点D在CB的延长线上，且ED=EC，如图1．试确定线段AE与DB的大小关系，并说明理由．
小明与同桌小聪讨论后，进行了如下解答：
（1）特殊情况，探索结论
当点E为AB的中点时，如图2，确定线段AE与DB的大小关系，请你直接写出结论：AE DB（填“＞”，“＜”或“=”）．
（2）一般情况，证明结论
如图3，过点E作EF∥BC，交AC于点F．
（请你继续完成对以上问题（1）中所填写结论的证明）
证明：
发布：2025/6/21 17:30:1组卷：91引用：3难度：0.2 -
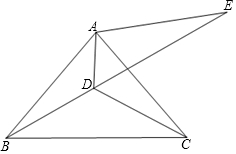2．如图，在△ABC中，AB=AC，∠BAC=80°，点D为△ABC内一点，∠ABD=∠ACD=20°，E为BD延长线上的一点，且AB=AE．
（1）求∠BAD的度数；
（2）求证：DE平分∠ADC；
（3）请判断AD，BD，DE之间的数量关系，并说明理由．发布：2025/6/21 1:30:2组卷：1216引用：5难度：0.4 -
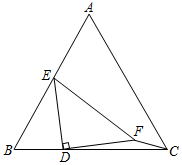3．如图，等边三角形ABC中，AB=6，D为BC上一点，且BD=2，E为AB上的一个动点，连接ED，将ED绕着点D顺时针旋转90°到DF，连接EF和FC，则CF的最小值为 ．发布：2025/6/21 19:30:1组卷：343引用：1难度：0.2
