我国著名数学家华罗庚说过“数缺形时少直观，形少数时难入微”，数形结合是解决数学问题的重要思想方法．例如，代数式|x-2|的几何意义是数轴上x所对应的点与2所对应的点之间的距离：因为|x+1|=|x-（-1）|，所以|x+1|的几何意义就是数轴上x所对应的点与-1所对应的点之间的距离．
（ⅰ）发现问题：代数式|x+1|+|x-2|的最小值是多少？
（ⅱ）探究问题：如图，点A、B、P分别表示数-1、2、x,AB=3，
∵|x+1|+|x-2|的几何意义是线段PA与PB的长度之和，
∴当点P在线段AB上时，PA+PB=3，当点P在点A的左侧或点B的右侧时，PA+PB＞3，
∴|x+1|+|x-2|的最小值是3．

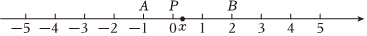
请你根据上述自学材料，探究解决下列问题：

解决问题：
（1）直接写出式子|x-3|+|x+2|的最小值是

5

5

；
（2）当a为何值时，代数式|x+a|+|x-4|的最小值是2；
（3）式子|x+3|+|x-1|+|x-5|的最小值是

8

8

．