数学课上大家一起研究三角形中位线性质定理：三角形两边中点的连线平行于第三边且等于第三边的一半．
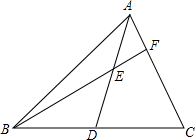
已知，如图1，在△ABC中，D、E分别是AB、AC的中点．
求证：DE∥BC且

DE

=

1

2

BC

．
​【定理探究】某数学小组有甲、乙、丙、丁四位同学．甲同学思考后说出了添加的辅助线：

甲：延长DE至点F，使EF=DE，连接CF．

【定理证明】请把甲同学说的辅助线补充到图1上，并根据他的思路证明三角形中位线性质定理；
【合作交流】通过交流乙、丙、丁三位同学又给出了三种不同的辅助线方法：
乙：延长DE到点F使EF=DE，连接FC、DC、AF．
丙：作AH⊥DE，延长HD使DG=HD，延长HE，使EF=HE．
丁：过点E作EG∥AB，交BC于点G，过点A作BC的平行线交GE于点F．
则三位同学所作的辅助线能证明三角形中位线性质定理的是

D

D

；
A．乙、丁 B．丙、丁 C．乙、丙 D．全正确
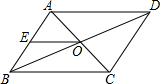
【定理应用】如图2，C，B两地被池塘隔开，不能直接测量它们之间的距离．测量员在地面上选了点A和点D，使AD∥BC，连接AB、DC．并分别找到AB和DC的中点M，N．若测得AD=am,MN=bm,则C，B两地间的距离

（2b-a）

（2b-a）

m.