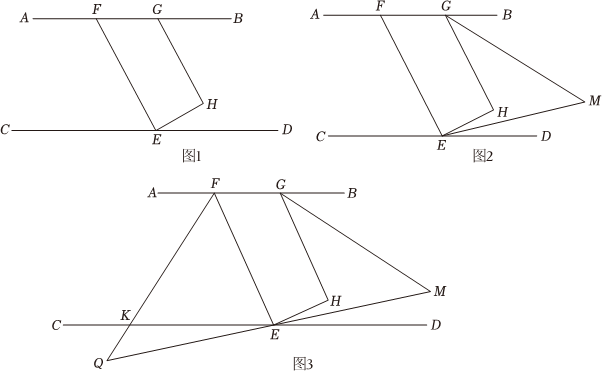
已知:AB∥CD,点E在CD上,点G、F在AB上,点H在AB、CD之间,连接FE、EH、HG,∠AGH=∠FED,FE⊥HE,垂足为点E.
(1)如图1,求证:HG⊥HE;
(2)如图2,GM平分∠HGB,EM平分∠HED,GM、EM交于点M,求证:∠GHE=2∠GME;
(3)如图3,在(2)的条件下,FK平分∠AFE交CD于点K,若∠KFE:∠MGH=13:5,FK与ME所在直线相交于点Q,求∠FQM的度数.
【答案】(1)见解答;
(2)见解答;
(3)45°.
(2)见解答;
(3)45°.
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/25 7:0:2组卷:87引用:1难度:0.4