如图，在▱ABCD中，O是对角线BD的中点，AD⊥BD，AB=5cm,AD=3cm,动点P从点A出发，以2cm/s的速度沿折线AB-BC向终点C运动，连接PO并延长交折线CD-DA于点Q，设点P的运动时间为t（s）．
（1）当点P在边AB上时，求证：△BOP≌△DOQ；
（2）当PQ与▱ABCD的边垂直时，求PQ的长；
（3）当以B、D、P、Q为顶点的四边形是矩形时，直接写出t的值；
（4）当直线PD把▱ABCD的面积分成1：3两部分时，直接写出线段PQ的长．
【考点】四边形综合题．
【答案】（1）证明过程详见解答；
（2）t=或；
（3）t=；
（4）PQ=或2．
（2）t=
5
2
17
10
（3）t=
9
10
（4）PQ=
2
13
3
5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/18 8:0:10组卷：37引用：1难度：0.5
相似题
-
1．在人教版八年级上册数学教材P53的数学活动中有这样一段描述：在四边形ABCD中，AD=CD，AB=CB，我们把这种两组邻边分别相等的四边形叫做“筝形”，如图（1）．
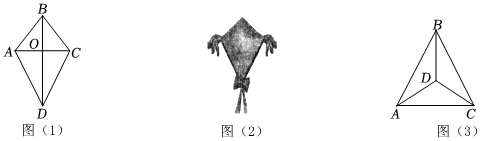
（1）知识应用：小风想要做一个如图（2）所示的风筝，他想先固定中间的“十字架”，再确定四周，从数学的角度看，小风确定“十字架”时应满足什么要求？并证明你的结论．
（2）知识拓展：如图（3）所示，如果D为△ABC内一点，BD平分∠ABC，且AD=CD，试证明：AB=CB．发布：2025/6/9 0:30:2组卷：72引用：1难度：0.2 -
2．矩形ABCD中，∠ACB=30°，△BEF中，∠BEF=90°，∠BFE=30°，BF=
AC，连接FD，点G是FD中点，将△BEF绕点B顺时针旋转α（0°＜α＜360°）．12
（1）如图1，若点B恰好在线段DF延长线上，AB=4，连接EG，求EG的长度；
（2）如图2，若点E恰好落在线段FD上，连接AG，证明：2（GD-GA）=DC；3
（3）如图3，若点E恰好落在线段AB延长线上，点M是线段AD上一点，3AM=DM，N是平面内一点，满足∠MND=∠FDC，已知AB=4，当△DMN是等腰三角形时，直接写出线段MN的长度．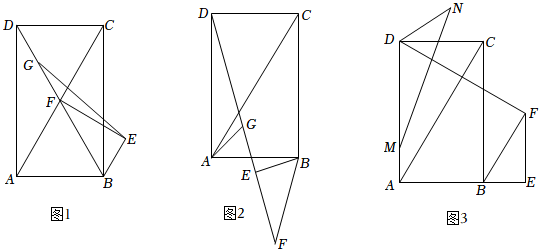
发布：2025/6/9 1:0:1组卷：118引用：1难度：0.1 -
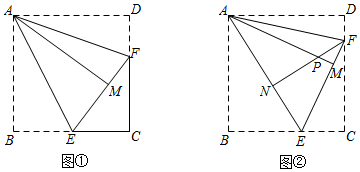3．问题情境：数学活动课上，老师组织同学们以“正方形”为主题开展数学活动．
动手实践：
（1）如图①，已知正方形纸片ABCD，勤奋小组将正方形纸片沿过点A的直线折叠，使点B落在正方形ABCD的内部，点B的对应点为点M，折痕为AE，再将纸片沿过点A的直线折叠，使AD与AM重合，折痕为AF，易知点E、M、F共线，则∠EAF=度．
拓展应用：
（2）如图②，腾飞小组在图①的基础上进行如下操作：将正方形纸片沿EF继续折叠，使得点C的对应点为点N，他们发现，当点E的位置不同时，点N的位置也不同，当点E在BC边的某一位置时，点N恰好落在折痕AE上．
①则∠CFE=度．
②设AM与NF的交点为点P，运用（1）、（2）操作所得结论，求证：△ANP≌△FNE．
解决问题：
（3）在图②中，若AB=3，请直接写出线段MP的长．发布：2025/6/9 2:0:7组卷：1098引用：9难度：0.3
