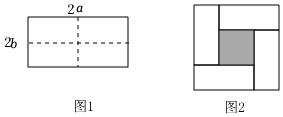
如图1所示的是一个长为2a,宽是2b的长方形，沿图中虚线用剪刀均分成四个同等大小的小长方形，然后按图2的方式拼成一个正方形．
（1）你认为图2中的阴影部分的正方形的边长等于 a-ba-b；
（2）请用两种不同的方法列代数式表示图2中阴影部分的面积．
方法一：S阴影=S正方形-4S长方形=（a+b）2-4ab=（a-b）2S阴影=S正方形-4S长方形=（a+b）2-4ab=（a-b）2；
方法二：S阴影=（a-b）2S阴影=（a-b）2．
（3）观察图2，你能写出（a+b）2，（a-b）2，ab这三个代数式之间的数量关系吗？
（4）当a=b=3，求阴影部分的面积．
a
【答案】a-b；S阴影=S正方形-4S长方形=（a+b）2-4ab=（a-b）2；S阴影=（a-b）2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/19 7:0:1组卷：444引用：6难度：0.6
