观察图片中的风筝,它们的主体部分可以看成是一个四边形,这类四边形的特征是两组邻边分别相等,我们把这样的四边形叫做“筝形”.
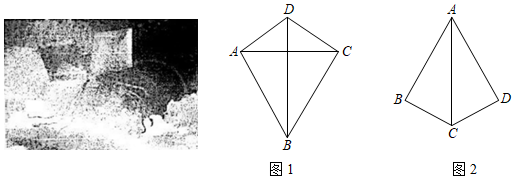
(1)提出猜想通过观察、测量等方法猜想筝形的对角线有什么性质,写出你的猜想 有一条对角线垂直平分另一条对角线有一条对角线垂直平分另一条对角线.(写出一个即可)
(2)证明猜想.(结合图1写出已知,求证,并证明).
(3)解决问题.如图2,在筝形ABCD中,∠DAB=60°,∠ABC=∠ADC=90°,AB=AD=6,求对角线AC的长.
【考点】四边形综合题.
【答案】有一条对角线垂直平分另一条对角线
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/27 3:0:8组卷:157引用:2难度:0.3
相似题
-
1.已知△ABC是等边三角形,四边形ADEF是菱形,∠ADE=120°(AD>AB).
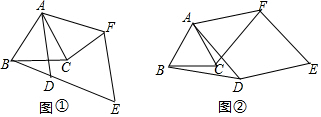
(1)如图①,当AD与边BC相交,点D与点F在直线AC的两侧时,BD与CF的数量关系为.
(2)将图①中的菱形ADEF绕点A旋转α(0°<α<180°),如图②.
Ⅰ.判断(1)中的结论是否仍然成立,请利用图②证明你的结论.
Ⅱ.若AC=4,AD=6,当△ACE为直角三角形时,直接写出CE的长度.发布:2025/6/25 7:30:2组卷:365引用:4难度:0.1 -
2.探究问题:
(1)方法感悟:
如图①,在正方形ABCD中,点E,F分别为DC,BC边上的点,且满足∠EAF=45°,连接EF,求证DE+BF=EF.
感悟解题方法,并完成下列填空:
证明:延长CB到G,使BG=DE,连接AG,
∵四边形ABCD为正方形,
∴AB=AD,∠ABC=∠D=90°,
∴∠ABG=∠D=90°,
∴△ADE≌△ABG.
∴AG=AE,∠1=∠2;
∵四边形ABCD为正方形,
∴∠BAD=90°,
∵∠EAF=45°,
∴∠2+∠3=∠BAD-∠EAF=90°-45°=45°.
∵∠1=∠2,
∴∠1+∠3=45°.
即∠GAF=∠.
又AG=AE,AF=AF,
∴△GAF≌.
∴FG=EF,
∵FG=FB+BG,
又BG=DE,
∴DE+BF=EF.
变化:在图①中,过点A作AM⊥EF于点M,请直接写出AM和AB的数量关系 ;
(2)方法迁移: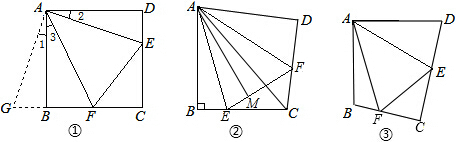
如图②,将Rt△ABC沿斜边AC翻折得到Rt△ADC,E,F分别是BC,CD边上的点,∠EAF=∠BAD,连接EF,过点A作AM⊥EF于点M,试猜想DF,BE,EF之间有何数量关系,并证明你的猜想.试猜想AM与AB之间的数量关系,并证明你的猜想.12
(3)问题拓展:
如图③,在四边形ABCD中,AB=AD,E,F分别为DC,BC上的点,满足∠EAF=∠DAB,试猜想当∠B与∠D满足什么关系时,可使得DE+BF=EF.请直接写出你的猜想(不必说明理由).猜想:∠B与∠D满足关系:.12发布:2025/6/24 19:0:1组卷:881引用:1难度:0.1 -
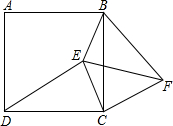 3.如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连接BE、CE、DE、BF、CF、EF.
3.如图,四边形ABCD是正方形,E是正方形ABCD内一点,F是正方形ABCD外一点,连接BE、CE、DE、BF、CF、EF.
(1)若∠EDC=∠FBC,ED=FB,试判断△ECF的形状,并说明理由.
(2)在(1)的条件下,当BE:CE=1:2,∠BEC=135°时,求BE:BF的值.
(3)在(2)的条件下,若正方形ABCD的边长为(3+3)cm,∠EDC=30°,求△BCF的面积.7发布:2025/6/24 17:30:1组卷:59引用:1难度:0.5


