 数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
数和形是数学的两个主要研究对象,我们经常运用数形结合、数形转化的方法解决一些数学问题.下面我们来探究“由数思形,以形助数”的方法在解决代数问题中的应用.
如图,将一个边长为1的正方形纸片分割成7个部分,部分①是边长为1的正方形纸片面积的一半,部分②是部分①面积的一半,部分③是部分②面积的一半,依次类推.
(1)图中阴影部分的面积为 164164;
(2)受此启发,得到12+14+18+⋯+126=63646364;
(3)联系拓广,得到12+14+18+⋯+12n=1-12n1-12n(用含n的式子表示);
(4)迁移应用:得到23+13×23+132×23+133×23+⋯+132023×23=1-1320241-132024(直接写出答案即可).
1
64
1
64
1
2
+
1
4
+
1
8
+
⋯
+
1
2
6
63
64
63
64
1
2
+
1
4
+
1
8
+
⋯
+
1
2
n
1
-
1
2
n
1
-
1
2
n
2
3
+
1
3
×
2
3
+
1
3
2
×
2
3
+
1
3
3
×
2
3
+
⋯
+
1
3
2023
×
2
3
1
-
1
3
2024
1
-
1
3
2024
【答案】;;;
1
64
63
64
1
-
1
2
n
1
-
1
3
2024
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/20 3:0:2组卷:369引用:2难度:0.5
相似题
-
1.如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,…,则在第n个图形中,互不重叠的三角形共有个 (用含n的代数式表示).
 发布:2025/6/17 4:30:1组卷:229引用:48难度:0.7
发布:2025/6/17 4:30:1组卷:229引用:48难度:0.7 -
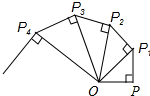 2.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )3发布:2025/6/17 9:30:1组卷:4123引用:15难度:0.7
2.如图,OP=1,过点P作PP1⊥OP且PP1=1,得OP1=;再过点P1作P1P2⊥OP1且P1P2=1,得OP2=2;又过点P2作P2P3⊥OP2且P2P3=1,得OP3=2…依此法继续作下去,得OP2017=( )3发布:2025/6/17 9:30:1组卷:4123引用:15难度:0.7 -
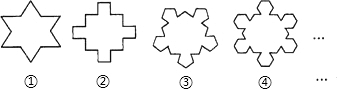
3.如图,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形(边数为20)是由正方形“扩展”而来的….以此类推,由正n边形“扩展”而来的多边形的边为 .
 发布:2025/6/17 5:0:1组卷:134引用:37难度:0.7
发布:2025/6/17 5:0:1组卷:134引用:37难度:0.7


