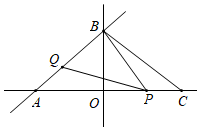
如图，在△ABC中，OA=8，OB=6，C点与A点关于直线OB对称，动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
（1）当OP=22时，△APQ≌△CBP，说明理由；
（2）当△PQB为等腰三角形时，求OP的长度．
【答案】2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/14 19:0:9组卷：571引用：3难度：0.6
相似题
-
1．如图，在△ABC中，∠BAC=90°，延长BA到点D，使AD=AB，点E、F分别为BC、AC的中点，请你在图中找出一组相等关系，使其满足上述所有条件，并加以证明．12发布：2025/1/24 8:0:2组卷：4引用：1难度：0.5 -
2．如图，在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在线段BC上，且AE=CF．
求证：∠AEB=∠CFB．发布：2025/1/24 8:0:2组卷：454引用：4难度：0.7 -
3．如图，在Rt△ABC中，∠C=∠BED=90°，且CD=DE，AD=BD，则∠B=．发布：2025/1/28 8:0:2组卷：10引用：0难度：0.7
