【实验观察】
（1）观察下列1×9，2×8，3×7，…，8×2，9×1两个数的乘积（两个乘数的和为10），猜想其中哪两个数的乘积最大（只写出结论即可）．
（2）观察下列45×55，46×54，47×53，…，54×46，55×45两个数的乘积（两个乘数的和为100），猜想其中哪两个数的乘积最大（只写出结论即可）．
（3）【猜想验证】根据上面活动给你的启示，猜想，如果两个正乘数的和为2n（其中n＞0），你认为两个乘数分别为多少时，两个乘数的乘积最大？用二次函数的知识说明你的猜想的正确性．
（4）【拓展应用】用长度为1.8m的竹签制作制作一个四边形的风筝（如图所示），风筝的骨架AB与CD（AB⊥CD），为了使风筝在空中能获得更大的浮力，要把风筝的表面积（四边形ADBC的面积）制作到最大．根据上面的结论，求当风筝的骨架AB、CD的长为多少时，风筝的表面积能达到最大？
【考点】二次函数综合题．
【答案】（1）5×5=25的乘积最大，理由见解答过程；
（2）50×50=2500的乘积最大，理由见解答过程；
（3）若两个数的和为m，当两个数分别为时，乘积最大，理由见解答过程；
（4）当AB=CD=0.9米时，风筝的表面积能达到最大．
（2）50×50=2500的乘积最大，理由见解答过程；
（3）若两个数的和为m，当两个数分别为
m
2
（4）当AB=CD=0.9米时，风筝的表面积能达到最大．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/13 0:0:8组卷：63引用：1难度：0.2
相似题
-
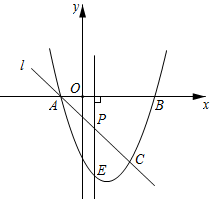1．如图，抛物线y=x2+bx+c与x轴交于A（-1，0），B（3，0）两点，过点A的直线l交抛物线于点C（2，m）．
（1）求抛物线的解析式．
（2）点P是线段AC上一个动点，过点P作x轴的垂线交抛物线于点E，求线段PE最大时点P的坐标．
（3）点F是抛物线上的动点，在x轴上是否存在点D，使得以点A，C，D，F为顶点的四边形是平行四边形？如果存在，请直接写出所有满足条件的点D的坐标；如果不存在，请说明理由．发布：2025/6/14 23:30:1组卷：4755引用：21难度：0.1 -
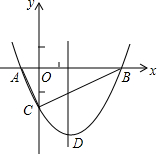2．如图，抛物线y=x2+bx-2与x轴交于A、B两点，与y轴交于C点，且A（-1，0）．12
（1）求抛物线的解析式及顶点D的坐标；
（2）判断△ABC的形状，证明你的结论；
（3）点M是抛物线对称轴上的一个动点，当△ACM周长最小时，求点M的坐标及△ACM的最小周长．发布：2025/6/15 6:30:1组卷：2010引用：14难度：0.5 -
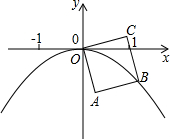3．边长为1的正方形OA1B1C1的顶点A1在x轴的正半轴上，如图将正方形OA1B1C1绕顶点O顺时针旋转75°得正方形OABC，使点B恰好落在函数y=ax2（a＜0）的图象上，则a的值为 ．发布：2025/6/14 23:30:1组卷：2330引用：24难度：0.7
