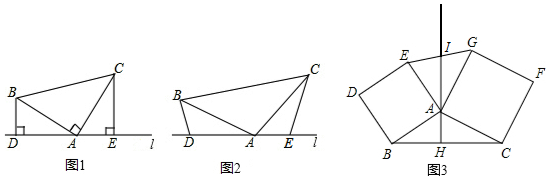
（1）如图1，已知：在△ABC中，∠BAC=90°，AB=AC，直线l经过点A，BD⊥l,CE⊥l,垂足分别为点D、E．证明：①∠CAE=∠ABD；②DE=BD+CE．
（2）如图2，将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在l上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问结论DE=BD+CE是否成立？若成立，请你给出证明；若不成立，请说明理由．
（3）如图3，过△ABC的边AB、AC向外作正方形ABDE和正方形ACFG，AH是BC边上的高，延长HA交EG于点I，求证：I是EG的中点．
【考点】四边形综合题．
【答案】（1）①证明过程见解答；
②证明过程见解答；
（2）成立：DE=BD+CE．证明过程见解答；
（3）证明过程见解答．
②证明过程见解答；
（2）成立：DE=BD+CE．证明过程见解答；
（3）证明过程见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/23 18:0:9组卷：951引用：4难度：0.4
相似题
-
1．如图1，在Rt△ABC中，∠ACB=90°，∠CAB=30°，点D在边AB上以CD为底边作等腰直角△CDP（点P，A在直线CD的两侧），射线CP交直线AB于点E．
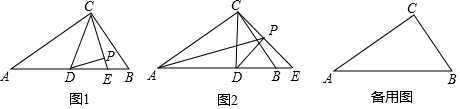
（1）若点D是AB的中点，且BC=2，求DP的长；
（2）当△CDE是等腰三角形时，求∠BCE的度数；
（3）如图2，设AP=a,求四边形ADPC面积的最小值．（用含a的式子表示）发布：2025/6/17 4:30:1组卷：26引用：1难度：0.4 -
2．如图，在菱形ABCD中，对角线AC，BD交于点O．
（1）若AB=5，AC=8，则菱形ABCD的面积是 ；
（2）点F在BC上，AF交BD于点E，若BE=BF，求证：CF=2OE；
（3）点P在射线AC上，且∠PDO=，若AC=16，AD=10，则DP的长为 ．12∠PCD
发布：2025/6/17 4:30:1组卷：164引用：2难度：0.1 -
3．将纸片△ABC沿DE折叠使点A落在点A'处．
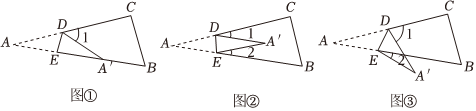
【感知】如图①，点A落在四边形BCDE的边BE上，则∠A与∠1之间的数量关系是 ；
【探究】如图②，若点A落在四边形BCDE的内部，则∠A与∠1+∠2之间的数量关系是 ；
【拓展】如图③，点A落在四边形BCDE的外部，若∠1=80°，∠2=24°，则∠A的大小为 ．发布：2025/6/17 4:30:1组卷：309引用：4难度：0.4
