如图，在矩形ABCD中，点E为边AD的中点，点F为AB上的一个动点，连接FE并延长，交CD的延长线于点G，以FG为底边在FG下方作等腰Rt△FHG，且∠FHG=90°．
（1）如图①，若点H恰好落在BC上，连接BE，EH．求证：AD=2AB；
（2）如图②，点H落在矩形ABCD内，连接CH，若AD=4，AB=3，求四边形FHCB面积的最大值．
【答案】（1）证明见解析；
（2）．
（2）
41
8
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/14 8:0:9组卷：108引用：2难度：0.5
相似题
-
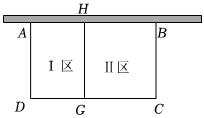1．为落实国家《关于全面加强新时代大中小学劳动教育的意见》，某校准备在校园里利用围墙（墙长9m）和21m长的篱笆墙，围成Ⅰ区、Ⅱ区两块矩形劳动实践基地（如图所示）．要使围成的两块矩形总种植面积最大，则BC应设计为 m.发布：2025/5/24 10:0:2组卷：192引用：1难度：0.6 -
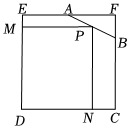2．如图，已知在边长为6的正方形FCDE中，A为EF的中点，点B在边FC上，且BF=2，连接AB，P是线段AB上的一动点，过点P作PM⊥DE，PN⊥DC，垂足分别为M，N，则矩形PNDM面积的最大值是 ．发布：2025/5/23 23:0:1组卷：73引用：1难度：0.5 -
3．如图Rt△ABC≌Rt△DEF，∠ACB=∠DFE=30°，AB=DE=a,且点B，C，F，E在一条直线上．
（1）沿着EB方向平移△DEF，当F点在线段BC上时，两个三角形重合部分的面积最大值是 ．
（2）继续沿直线CF平移△DEF，如图2，求图中阴影部分面积的最大值．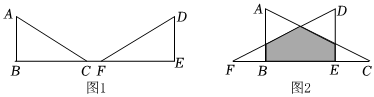
发布：2025/5/24 1:0:1组卷：140引用：1难度：0.5
