阅读下列材料：
我们把多项式a²+2ab+b²及a²-2ab+b²叫做完全平方公式，如果一个多项式不是完全平方公式，我们常做如下变形：先添加一个适当的项，使式子中出现完全平方式，再减去这个项，使整个式子的值不变，这种方法叫做配方法．配方法是一种重要的解决问题的数学方法，可以求代数式的最大值或最小值．
例如：求代数式x²+2x-4的最小值．
x²+2x-4=（x²+2x+1）-5=（x+1）²-5，可知当x=-1 时，x²+2x-4有最小值，最小值是-5．
再例如：求代数式-3x²+6x-4的最大值．
-3x²+6x-4=-3（x²-2x+1）-4+3=-3（x-1）²-1，可知当x=1时，-3x²+6x-4有最大值，最大值是-1.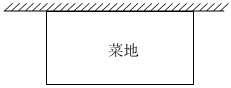
（1）【直接应用】代数式x²+4x-3的最小值为

-7

-7

；
（2）【类比应用】若多项式M=a²+b²-2a+3b+2023，试求M的最小值；
（3）【知识迁移】如图，学校打算用长20米的篱笆围一个长方形的菜地，菜地的一面靠墙（墙足够长），求围成的菜地的最大面积．