小华同学学习函数知识后，对函数y=4x2（-1＜x≤0） -4x（x≤-1或x＞0）
通过列表、描点、连线，画出了如图1所示的图象．
4 x 2 （ - 1 ＜ x ≤ 0 ） |
- 4 x （ x ≤ - 1 或 x ＞ 0 ） |
| x | ⋯ | -4 | -3 | -2 | -1 | - 3 4 |
- 1 2 |
- 1 4 |
0 | 1 | 2 | 3 | 4 | ⋯ |
| y | ⋯ | 1 | 4 3 |
2 | 4 | 9 4 |
1 | 1 4 |
0 | -4 | -2 | - 4 3 |
-1 | ⋯ |
（1）【观察发现】
①写出函数的两条性质：
函数有最大值为4
函数有最大值为4
； 当x＞0时y随x的增大而增大
当x＞0时y随x的增大而增大
；②若函数图象上的两点（x1，y1），（x2，y2）满足x1+x2=0，则y1+y2=0一定成立吗？
不一定成立
不一定成立
．（直接填写“一定成立”或“不一定成立”）（2）【延伸探究】如图2，将过A（-1，4），B（4，-1）两点的直线向下平移n个单位长度后（n≥0），得到直线l与函数y=-
4
x
①求当n=3时，直线l的解析式和△PAB的面积；
②请直接写出表示△PAB面积的代数式（用n表达）．
【考点】二次函数综合题．
【答案】函数有最大值为4；当x＞0时y随x的增大而增大；不一定成立
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/4 9:0:2组卷：151引用：1难度：0.3
相似题
-
1．如图，已知抛物线y=ax2+bx-2与x轴的两个交点是A（4，0），B（1，0），与y轴的交点是C．
（1）求该抛物线的解析式；
（2）在直线AC上方的该抛物线上是否存在一点D，使得△DCA的面积最大？若存在，求出点D的坐标及△DCA面积的最大值；若不存在，请说明理由；
（3）设抛物线的顶点是F，对称轴与AC的交点是N，P是在AC上方的该抛物线上一动点，过P作PM⊥x轴，交AC于M．若P点的横坐标是m.问：
①m取何值时，过点P、M、N、F的平面图形不是梯形？
②四边形PMNF是否有可能是等腰梯形？若有可能，请求出此时m的值；若不可能，请说明理由．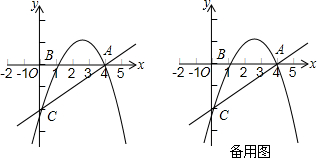
发布：2025/1/2 8:0:1组卷：83引用：1难度：0.5 -
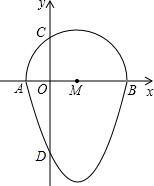2．如图，我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”．已知点A、B、C、D分别是“果圆”与坐标轴的交点，抛物线的解析式为y=x2-2x-3，AB为半圆的直径，则这个“果圆”被y轴截得的弦CD的长为．发布：2024/12/23 17:30:9组卷：3749引用：38难度：0.4 -
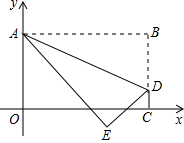3．如图，将矩形OABC置于平面直角坐标系中，点A的坐标为（0，4），点C在x轴上，点D（3，1）在BC上，将矩形OABC沿AD折叠压平，使点B落在坐标平面内，设点B的对应点为点E．若抛物线y=ax2-45ax+10（a≠0且a为常数）的顶点落在△ADE的内部，则a的取值范围是（ ）5发布：2024/12/26 1:30:3组卷：2679引用：7难度：0.7
