现有一四边形ABCD，借助此四边形作平行四边形EFGH，两位同学提供了如下方案，对于方案Ⅰ、Ⅱ，下列说法正确的是（ ）
方案Ⅰ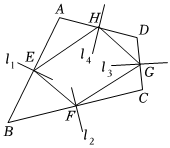 作边AB，BC，CD，AD的垂直平分线l1，l2，l3，l4，分别交AB，BC，CD，AD于点E，F，G，H，顺次连接这四点围成的四边形EFGH即为所求． |
方案Ⅱ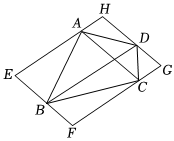 连接AC，BD，过四边形ABCD各顶点分别作AC，BD的平行线EF，GH，EH，FG，这四条平行线围成的四边形EFGH即为所求． |
【考点】平行四边形的性质；线段垂直平分线的性质．
【答案】C
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/1 8:0:9组卷：284引用：5难度：0.7
相似题
-
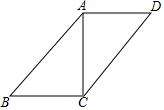1．如图，▱ABCD中，BC=8，AB=10，BC⊥AC，则▱ABCD的面积为．发布：2025/6/10 0:0:1组卷：44引用：2难度：0.5 -
2．一个平行四边形的一条边长是9，两条对角线长分别是12，6
，则这个平行四边形的一条边上的高为（ ）5发布：2025/6/9 23:30:1组卷：275引用：3难度：0.7 -
3．如图，在平行四边形ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上，连接EF、CF，以下结论：
①∠DCF=∠BCD；12
②EF=CF；
③∠DFE=4∠AEF；
④S△ABC＜2S△CEF．
一定成立的是（ ）发布：2025/6/9 22:30:2组卷：309引用：5难度：0.4
