某企业计划每天生产甲、乙两种品牌的电器分别为30台和20台，且当天生产的电器均能在市场上售出．根据市场调查反馈，在一段时间内乙电器的需求量较大，该企业决定在保持日生产总量不变的条件下，每天增加生产乙电器x台．这样发现：日销售两种电器的总利润W（元）与x（台）满足如下函数关系式：W=ax2+bx+16000，在生产销售过程中，还可以获得如下数据：
| x（台） | 5 | 10 |
| W（元） | 16250 | 16000 |
（2）若实际每天生产乙种电器的台数不低于甲种电器的1.4倍，求W的最大值；
（3）若在生产过程中，每台电器均可以节约m元（m为整数）的成本，设此时日销售总利润为Q（元），该企业的财务部门，经过核算发现：当Q大于17220元时，有3种不同的生产方案，求m的值．
【考点】二次函数的应用；二元一次方程组的应用．
【答案】（1）a=-10，b=100；
（2）W的最大值为16000元；
（3）m=20．
（2）W的最大值为16000元；
（3）m=20．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/12 9:0:2组卷：31引用：2难度：0.5
相似题
-
1．某果园有100棵橙子树，平均每棵树结600个橙子，现准备多种一些橙子树以提高果园产量，但是如果多种树，那么树之间的距离和每一棵树所接受的阳光就会减少．根据经验估计，每多种一棵树，平均每棵树就会少结5个橙子，假设果园多种了x棵橙子树．
（1）直接写出平均每棵树结的橙子个数y（个）与x之间的关系；
（2）果园多种多少棵橙子树时，可使橙子的总产量最大？最大为多少个？发布：2025/6/16 17:30:2组卷：4262引用：11难度：0.3 -
2．某商场购进一种每件价格为90元的新商品，在商场试销时发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系．
（1）求出y与x之间的函数关系式；
（2）写出每天的利润W与销售单价x之间的函数关系式，并求出售价定为多少时，每天获得的利润最大？最大利润是多少？发布：2025/6/16 9:0:1组卷：2829引用：17难度：0.8 -
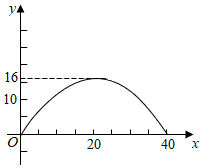3．如图，某抛物线型桥拱的最大高度为16米，跨度为40米，如图所示建立平面直角坐标系，则该抛物线对应的函数关系式为 ．发布：2025/6/16 12:0:1组卷：651引用：3难度：0.8
