某工厂生产A型产品，每件成本为20元，当A型产品的销售单价为x元时，销售量为y万件．要求每件A型产品的销售单价不低于20元且不高于28元．经市场调查发现，y与x之间满足一次函数关系，且当x=23时，y=34；x=25时，y=30．
（1）求y与x的函数关系式，并写出自变量x的取值范围；
（2）若某次销售刚好获得182万元的利润，则每件A型产品的销售单价是多少元？
（3）设该工厂销售A型产品所获得的利润为w万元，将该产品的销售单价定为多少元时，才能使销售该产品所获得的利润最大？最大利润是多少万元？
【答案】（1）y与x的函数关系式为y=-2x+80，自变量x的取值范围是20≤x≤28；
（2）每件A型产品的销售单价是27元；
（3）该产品的销售单价定为28元时，才能使销售该产品所获得的利润最大，最大利润是192万元．
（2）每件A型产品的销售单价是27元；
（3）该产品的销售单价定为28元时，才能使销售该产品所获得的利润最大，最大利润是192万元．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/7 8:0:9组卷：121引用：4难度：0.6
相似题
-
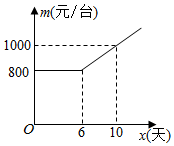1．某企业接到生产一批设备的订单，要求不超过12天完成．这种设备的出厂价为1200元/台，该企业第一天生产22台设备，第二天开始，每天比前一天多生产2台．若干天后，每台设备的生产成本将会增加，设第x天（x为整数）的生产成本为m（元/台），m与x的关系如图所示．
（1）若第x天可以生产这种设备y台，则y与x的函数关系式为 ，x的取值范围为 ；
（2）第几天时，该企业当天的销售利润最大？最大利润为多少？
（3）求当天销售利润低于10800元的天数．发布：2025/6/17 7:0:2组卷：2816引用：13难度：0.4 -
2．在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB=x m.
（1）若花园的面积为192m2，求x的值；
（2）若在P处有一棵树与墙CD，AD的距离分别是15m和6m,要将这棵树围在花园内（含边界，不考虑树的粗细），求花园面积S的最大值．发布：2025/6/17 7:0:2组卷：6613引用：117难度：0.1 -
3．青岛十九中新校广场上拟建造一圆形喷水池，在水池中央垂直于水面处要安装一个柱子OA，水流由柱子顶端A处的喷头喷出，喷出的水流呈抛物线形，O点恰好在水面中心，OA为1.5m,水流最高点为B，AB与水平面成45°角，B点距离水面的垂直高度为3.5m.
（1）按如图所示的平面直角坐标系，求抛物线的解析式；
（2）喷水池的半径至少为多少米，才能使水流不至于落到水池外？发布：2025/6/17 7:30:2组卷：147引用：2难度：0.6
