如图，矩形ABCD中，AB=10，BC=20，点M以每秒1个单位长度的速度沿AB从点A向点B运动，点N以每秒4个单位长度的速度沿BC从点B向点C运动，点P以每秒2个单位长度的速度沿CD从点C向点D运动，三动点同时出发，设运动时间为t秒，当点N到达点C时，三点同时停止运动．点B关于MN的对称点为点Q，连接MN，NP，MQ，NQ．
（1）当t为何值时，四边形MBNQ为正方形？并说明理由；
（2）若以点M，N，B为顶点的三角形与以点N，P，C为顶点的三角形相似，求t的值．

【答案】见试题解答内容

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/10/1 4:0:1组卷：375引用：2难度：0.5

相似题

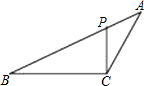1．如图，△ABC中，P为AB上一点，在下列四个条件中：
①∠ACP=∠B；②∠APC=∠ACB；③AC²=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（　　）
A．①②③ B．①③④ C．②③④ D．①②④
发布：2025/6/17 4:0:1组卷：692引用：46难度：0.7
解析
2．如图，AB∥CD，AE∥FD，AE，FD分别交BC于点G，H，则图中共有相似三角形（　　）
A．4对 B．5对 C．6对 D．7对
发布：2025/6/17 0:0:1组卷：564引用：51难度：0.9
解析
3．如图，在平面直角坐标系中有两点A（4，0）、B（0，2），如果点C在x轴上（C与A不重合），当点C的坐标为
或
时，使得由点B、O、C组成的三角形与△AOB相似（至少找出两个满足条件的点的坐标）．
发布：2025/6/17 5:30:3组卷：2068引用：19难度：0.9
解析

1．如图，△ABC中，P为AB上一点，在下列四个条件中：①∠ACP=∠B；②∠APC=∠ACB；③AC2=AP•AB；④AB•CP=AP•CB，能满足△APC与△ACB相似的条件是（ ）