阅读下列两则材料，回答问题
材料一：我们将（a+b）与（a-b）称为一对“对偶式”
因为（a+b）（a-b）=（a）2-（b）2=a-b,所以构造“对偶式”相乘可以有效地将（a+b）和（a-b）中的“”去掉
例如：已知25-x-15-x=2，求25-x+15-x的值．
解：（25-x-15-x）×（25-x+15-x）=（25-x）-（15-x）=10
∵25-x-15-x=2，
∴25-x+15-x=5
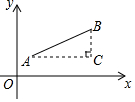
材料二：如图，点A（x1，y1），点B（x2，y2），以AB为斜边作Rt△ABC，
则C（x2，y1），于是AC=|x1-x2|，BC=|y1-y2|，所以
AB=（x1-x2）2+（y1-y2）2．
反之，可将代数式（x1-x2）2+（y1-y2）2的值看作点（x1，y1）到点（x2，y2）的距离．例如
x2-2x+y2+2y+2=（x2-2x+1）+（y2+2y+1）=（x-1）2+（y+1）2=（x-1）2+[y-（-1）]2．
所以可将代数式x2-2x+y2+2y+2的值看作点（x,y）到点（1，-1）的距离．
（1）利用材料一，解关于x的方程：20-x-4-x=2，其中x≤4；
（2）①利用材料二，求代数式x2-2x+y2-16y+65+x2+4x+y2-4y+8的最小值，并求出此时y与x的函数关系式，写出x的取值范围；
②将①所得的y与x的函数关系式和x的取值范围代入y=2x2+5x+12+2x2+3x+6中解出x,直接写出x的值．
a
b
a
b
a
b
a
b
a
b
a
b
a
b
25
-
x
15
-
x
25
-
x
15
-
x
25
-
x
15
-
x
25
-
x
15
-
x
25
-
x
15
-
x
25
-
x
15
-
x
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
（
x
1
-
x
2
）
2
+
（
y
1
-
y
2
）
2
x
2
-
2
x
+
y
2
+
2
y
+
2
（
x
2
-
2
x
+
1
）
+
（
y
2
+
2
y
+
1
）
（
x
-
1
）
2
+
（
y
+
1
）
2
（
x
-
1
）
2
+
[
y
-
（
-
1
）
]
2
x
2
-
2
x
+
y
2
+
2
y
+
2
20
-
x
4
-
x
x
2
-
2
x
+
y
2
-
16
y
+
65
+
x
2
+
4
x
+
y
2
-
4
y
+
8
2
x
2
+
5
x
+
12
2
x
2
+
3
x
+
6
【考点】配方法的应用．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/2 0:0:1组卷：1215引用：4难度：0.6
