【图形定义】
有一条高线相等的两个三角形称为等高三角形．
例如：如图（1）．在△ABC和△A′B′C′中，AD和A′D′分别是BC和B′C′边上的高线，且AD=A′D′，则△ABC和△A′B′C′是等高三角形．
【性质探究】
如图（1），用S△ABC，S△A′B′C′分别表示△ABC和△A′B′C′的面积．
则S△ABC=12BC•AD，S△A′B′C′=12B′C′•A′D′，
∵AD=A′D′
∴S△ABC：S△A′B′C=BC：B′C′．
【性质应用】
（1）如图②，D是△ABC的边BC上的一点．若BD=3，DC=4，则S△ABD：S△ADC=3：43：4；
（2）如图③，在△ABC中，D，E分别是BC和AB边上的点．若BE：AB=1：2，CD：BC=1：3，S△ABC=1，求△BEC和△CDE的面积．
1
2
1
2
【考点】三角形综合题．
【答案】3：4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/17 8:0:9组卷：173引用：4难度：0.5
相似题
-
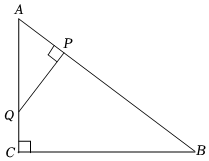1．如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，动点P从点A出发沿线段AB以每秒3个单位长的速度运动至点B，过点P作PQ⊥AB交射线AC于点Q，设点P的运动时间为t秒（t＞0）．
（1）线段AQ的长为 ，线段PQ的长为 .（用含t的代数式表示）
（2）当△APQ与△ABC的周长的比为1：4时，求t的值．
（3）设△APQ与△ABC重叠部分图形的面积为S，求S与t之间的函数关系式．发布：2025/6/25 4:0:1组卷：19引用：1难度：0.3 -
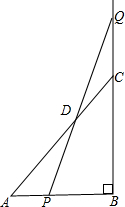2．已知等腰直角△ABC的直角边AB=BC=10cm,点P，Q分别从A．C两点同时出发，均以1cm/s的相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t,△PCQ的面积为S．
（1）求出S关于t的函数关系式．
（2）当点P在线段AB上时，点P运动几秒时，S△PCQ=S△ABC？14
（3）作PE⊥AC于点E，当点P．Q运动时，线段DE的长度是否改变？证明你的结论．发布：2025/6/23 23:0:10组卷：243引用：1难度：0.1 -
3．如图，在△ABC中，BC=5，AD⊥BC，BE⊥AC，AD，BE相交于点O，BD：CD=2：3，且AE=BE．
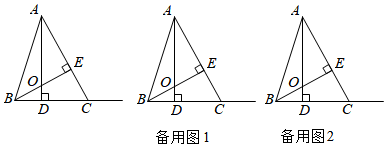
（1）求线段AO的长；
（2）动点P从点O出发，沿线段OA以每秒1个单位长度的速度向终点A运动，动点Q从点B出发沿射线BC以每秒4个单位长度的速度运动．P，Q两点同时出发，当点P到达A点时，P，Q两点同时停止运动．设点P的运动时间为t秒，△AOQ的面积为S，请用含t的式子表示S，并直接写出相应的t的取值范围；
（3）在（2）的条件下，点F是直线AC上的一点，且CF=BO，是否存在t值，使以点B，O，P为顶点的三角形与以点F，C，Q为顶点的三角形全等？若存在，请直接写出符合条件的t值；若不存在，请说明理由．发布：2025/6/25 5:0:1组卷：191引用：3难度：0.4
