教材中有这样一道题：如图1，四边形ABCD是正方形，G是BC上的任意一点，DE⊥AG于点E，BF∥DE，且交AG于点F．求证：AF-BF=EF．

小明通过证明△AED≌△BFA解决了问题，在此基础上他进一步提出了以下问题，请你解答．
（1）若图1中的点G为CB延长线上一点，其余条件不变，如图2所示，猜想此时AF，BF，EF之间的数量关系，并证明你的结论．
（2）将图1中的△ABF绕点A逆时针旋转，使得AB与AD重合，记此时点F的对应点为点F'，如图3所示，若正方形的边长为3，求EF'的长度．

【答案】证明见解答过程；
（1）AF+BF=EF；
（2）EF'=3．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/7/9 8:0:8组卷：1033引用：5难度：0.2

相似题

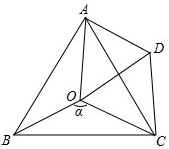1．如图，点O是等边△ABC内一点，∠AOB=105°，∠BOC等于α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．
（1）求证：△COD是等边三角形．
（2）求∠OAD的度数．
（3）探究：当α为多少度时，△AOD是等腰三角形？
发布：2025/6/15 9:30:1组卷：2351引用：8难度：0.5
解析
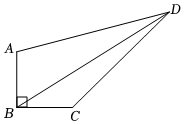2．如图，在四边形ABCD中，∠ABC=90°，AB=BC=1，CD=2
2
，AD=
10
．
（1）求∠BCD的度数；
（2）连接BD，求BD的长．
发布：2025/6/15 9:0:1组卷：160引用：3难度：0.7
解析
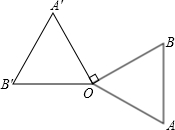3．如图，等边三角形AOB绕点O顺时针旋转到△A′OB′的位置，且OA′⊥OB，则△AOB旋转了
度．
发布：2025/6/15 9:0:1组卷：88引用：4难度：0.7
解析

1．如图，点O是等边△ABC内一点，∠AOB=105°，∠BOC等于α，将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形．（2）求∠OAD的度数．（3）探究：当α为多少度时，△AOD是等腰三角形？