某校数学社团活动时，徐老师提出了如下问题：
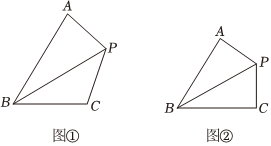
已知：如图①，在四边形ABCP中，∠ABC=60°，PB平分∠ABC，∠A+∠C=180°．求证：AB+BC=3BP．
小刚反复思考，没有找到思路．
李芳想，如果将四边形ABCP特殊化，能否找到思路呢？
（1）于是，她由特殊情况入手，添加条件“∠A=∠C”，如图②，可证：AB+BC=3BP．请你完成此证明．
（2）请你根据问题（1）受到的启发，在图①中添加适当的辅助线，解决上面的问题．
AB
+
BC
=
3
BP
AB
+
BC
=
3
BP
【考点】全等三角形的判定与性质；角平分线的性质．
【答案】（1）见解答；
（2）见解答．
（2）见解答．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：143引用：1难度：0.5
相似题
-
1．情境观察
将矩形ABCD纸片沿对角线AC剪开，得到△ABC和△A′C′D，如图1所示．将△A′C′D的顶点A′与点A重合，并绕点A按逆时针方向旋转，使点D、A（A′）、B在同一条直线上，如图2所示．
观察图2可知：与BC相等的线段是，∠CAC′=°．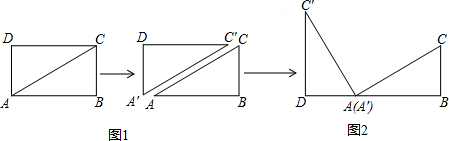
问题探究
如图3，△ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，过点E、F作射线GA的垂线，垂足分别为P、Q．试探究EP与FQ之间的数量关系，并证明你的结论．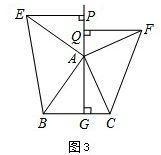
发布：2025/6/24 14:30:1组卷：446引用：11难度：0.3 -
2．如图：在△ABC中，AD⊥BC于D，AD=BD，CD=DE，E是AD上一点，连接BE并延长交AC于点F．求证：（1）BE=AC；（2）BF⊥AC．发布：2025/6/24 14:30:1组卷：208引用：4难度：0.3 -
3．如图，∠ADC=
°．
发布：2025/6/24 13:0:11组卷：1196引用：21难度：0.7
