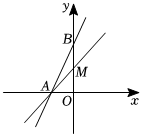
如图，在平面直角坐标系中，函数y=2x+6的图象分别交x轴，y轴于A，B两点，过点A的直线交y轴正半轴于点M，且点M为线段OB的中点．
（1）求直线AM的函数解析式；
（2）试在直线AM上找一点P，使得S△ABP=S△AOB，请求出点P的坐标；
（3）若点N为坐标平面内任意一点，在坐标平面内是否存在这样的点N，使以A，B，M，N为顶点的四边形是平行四边形？若存在，请直接写出所有点N的坐标；若不存在，请说明理由．
【考点】一次函数综合题．
【答案】（1）y=x+3；
（2）（-9，-6）或（3，6）；
（3）存在，（-3，-3），（-3，3）或（3，9）．
（2）（-9，-6）或（3，6）；
（3）存在，（-3，-3），（-3，3）或（3，9）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/27 8:0:9组卷：109引用：4难度：0.5
相似题
-
1．某工厂有14m长的旧墙一面，现在准备利用这面旧墙，建造平面图形为矩形，面积为126m2的厂房，工程条件为：①建1m新墙的费用为a元；②修1m旧墙的费用为
元；③拆去1m旧墙，用所得材料建造1m新墙的费用为a4元．经过讨论有两种方案：（Ⅰ）利用旧墙的一段xm（x＜14）为矩形厂房一面的边长；（Ⅱ）矩形厂房利用旧墙的一面边长为x（x≥14）．问：如何利用旧墙，即x为多少米时，建墙费用最省？（Ⅰ）（Ⅱ）两种方案哪个更好？a2发布：2025/5/28 13:30:2组卷：39引用：1难度：0.9 -
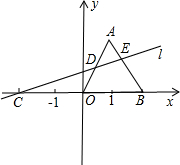2．如图，△AOB为正三角形，点B坐标为（2，0），过点C（-2，0）作直线L交AO于D，交AB于E，且使△ADE和△DCO的面积相等，求直线L的函数解析式．发布：2025/5/28 19:0:1组卷：695引用：3难度：0.1 -
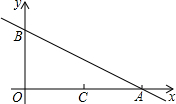3．如图，已知点A与点B的坐标分别为（4，0），（0，2）．
（1）求直线AB的解析式；
（2）过点C（2，0）的直线（与x轴不重合）交y轴于点P，若截得的△PCO与△AOB全等，求点P的坐标．发布：2025/5/28 19:30:2组卷：42引用：3难度：0.3
