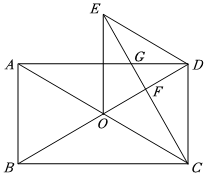
如图，矩形ABCD的对角线AC与BD相交于点O，CD∥OE，直线CE是线段OD的垂直平分线，CE分别交OD，AD于点F，G，连接DE．
（1）判断四边形OCDE的形状，并说明理由；
（2）当CD=4时，求EG的长．
【考点】矩形的性质；线段垂直平分线的性质．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/5/18 8:0:8组卷：3642引用：18难度：0.7
相似题
-
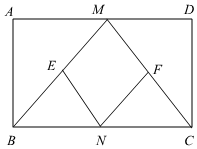1．已知：如图，在矩形ABCD中，M、N分别是边AD、BC的中点，E、F分别是线段BM、CM的中点．
（1）求证：△ABM≌△DCM；
（2）填空：当AB：AD=时，四边形MENF是正方形．发布：2025/6/19 19:30:1组卷：1301引用：73难度：0.5 -
2．矩形ABCD中，AB=2，BC=1，点P是直线BD上一点，且DP=DA，直线AP与直线BC交于点E，则CE=
．发布：2025/6/19 19:30:1组卷：884引用：65难度：0.5 -
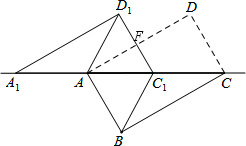3．如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1，连接AD1、BC1．若∠ACB=30°，AB=1，CC1=x,
△ACD与△A1C1D1重叠部分的面积为s,则下列结论：
①△A1AD1≌△CC1B；
②当x=1时，四边形ABC1D1是菱形；
③当x=2时，△BDD1为等边三角形；
④s=（x-2）2（0＜x＜2）；38
其中正确的是（填序号）．发布：2025/6/19 19:30:1组卷：1439引用：69难度：0.7
