如图，方格纸中每个小方格都是边长为1的正方形，我们把以格点的连线为边的多边形称为“格点多边形”，如图中四边形ABCD就是一个“格点四边形”．
（1）求图中四边形ABCD的面积；
（2）在图中的方格纸中画一个格点四边形，使该四边形与原四边形ABCD关于直线l成轴对称；
（3）P为直线l上一点，连接BP、AP，使得BP+AP最小，画出点P的位置．
（4）Q为直线l上一点，连接BQ、CQ，使得|BQ-CQ|最大，画出点Q的位置．

【答案】（1）6．
（2）见解答．
（3）见解答．
（4）见解答．

【解答】

【点评】

声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。

发布：2024/9/22 3:0:20组卷：335引用：3难度：0.5

相似题

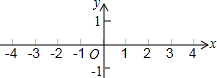1．在平面直角坐标系中，已知点A（-3，1），B（-1，0），C（-2，-1），请在图中画出△ABC，并画出与△ABC关于y轴对称的图形．
发布：2025/6/24 2:0:1组卷：472引用：45难度：0.7
解析
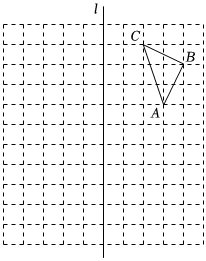2．如图，在边长为1个单位长度的小正方形网格中，给出了△ABC（顶点是网格线的交点）．
（1）请画出△ABC关于直线l对称的△A₁B₁C₁；
（2）将线段AC向左平移3个单位，再向下平移5个单位，画出平移得到的线段A₂C₂，并以它为一边作一个格点△A₂B₂C₂，使A₂B₂=C₂B₂．
发布：2025/6/24 3:0:1组卷：1729引用：53难度：0.7
解析
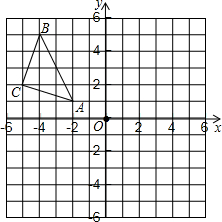3．作图题：（不要求写作法）如图，△ABC在平面直角坐标系中，其中，点A、B、C的坐标分别为A（-2，1），B（-4，5），C（-5，2）．
（1）作△ABC关于直线l：x=-1对称的△A₁B₁C₁，其中，点A、B、C的对应点分别为A₁、B₁、C₁；
（2）写出点A₁、B₁、C₁的坐标．
发布：2025/6/24 3:30:1组卷：942引用：52难度：0.5
解析

1．在平面直角坐标系中，已知点A（-3，1），B（-1，0），C（-2，-1），请在图中画出△ABC，并画出与△ABC关于y轴对称的图形．