在△ABC中，AB=BC=2，∠ABC=120°，将△ABC绕点B顺时针旋转角α（0°＜α＜90°）得△A1BC1，A1B交AC于点E，A1C1分别交AC、BC于D、F两点．
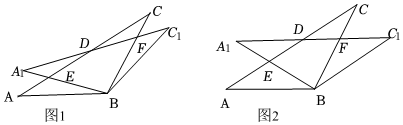
（1）如图1观察并猜想，在旋转过程中，线段EA1与FC有怎样的数量关系？证明你的结论；
（2）如图2，当α=30°时，试判断四边形BC1DA的形状，并请说明理由．
【答案】（1）EA1=CF；（2）四边形BC1DA是菱形．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/12 8:0:9组卷：32引用：2难度：0.5
相似题
-
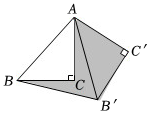1．如图，在△ABC中，∠C=90°，，将△ABC绕点A逆时针方向旋转60°到△ABC'的位置，则图中阴影部分的面积是 ．AC=BC=2发布：2025/6/8 6:30:2组卷：293引用：6难度：0.6 -
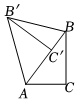2．如图，在Rt△ABC中，∠C=90°，将△ABC绕点A逆时针旋转n°（0＜n＜90）后得到△AB'C'，点C'恰好落在线段AB上，连接BB'，若∠BB′C′=25°，则n的大小为（ ）发布：2025/6/8 6:30:2组卷：135引用：2难度：0.7 -
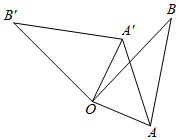3．如图，在△AOB中，AO=1，BO=AB=．将△AOB绕点O逆时针方向旋转90°，得到△A′OB′，连接AA′．则线段AA′的长为（ ）32发布：2025/6/8 7:0:2组卷：2013引用：19难度：0.8
