将一个矩形纸片OABC放在平面直角坐标系中，点O（0，0），点A（3，0），点C（0，6），点P在边OC上（点P不与点O，C重合），折叠该纸片，使折痕所在的直线经过点P，并与x轴的正半轴相交于点Q，且∠OPQ=30°，点O的对应点O'落在第一象限；设OQ=t.
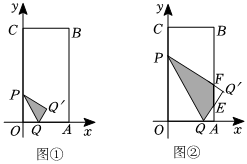
（1）如图①，当t=1时，求∠OQA的大小和点O'的坐标；
（2）如图②，若折叠后重合部分为四边形，O′Q，O′P分别与边AB相交于点E，F，试用含有t的式子表示OE的长，并直接写出t的取值范围．
【答案】（1）O′（，）；（2）EO′=3t-6（2＜t＜3）．
3
2
3
2
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/6/19 8:0:9组卷：223引用：3难度：0.6
相似题
-
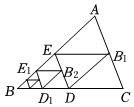1．如图，将△ABC沿着过BC的中点D的直线折叠，使点B落在AC边上的B1处，称为第一次操作，折痕DE到AC的距离为h1；还原纸片后，再将△BDE沿着过BD的中点D1的直线折叠，使点B落在DE边上的B2处，称为第二次操作，折痕D1E1到AC的距离记为h2；按上述方法不断操作下去…，经过第n次操作后得到折痕Dn-1En-1，到AC的距离记为hn．若h1=1，则hn的值为 ．发布：2025/5/24 9:0:1组卷：212引用：5难度：0.5 -
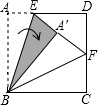2．如图，在正方形纸片ABCD上，E是AD上一点（不与点A，D重合）．将纸片沿BE折叠，使点A落在点A处，延长EA'交CD于点F，则∠EBF=（ ）发布：2025/5/24 8:0:1组卷：330引用：7难度：0.7 -
3．如图，正方形纸片ABCD，P为正方形AD边上的一点（不与点A，点D重合）．将正方形纸片折叠，使点B落在点P处，点C落在点G处，PG交DC于点H，折痕为EF，连接BP，BH，BH交EF于点M，连接PM．下列结论：①BE=PE；②BP=EF；③PB平分∠APG；④PH=AP+HC；⑤MH=MF，其中正确结论的个数是（ ）发布：2025/5/24 9:0:1组卷：1462引用：15难度：0.4
