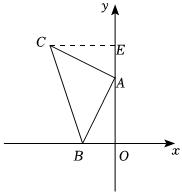
如图，平面直角坐标系中点B（-2，0），点A（0，5），以点A为直角顶点在第二象限内作等腰直角三角形ABC，过点C作CE垂直于y轴，垂足为点E，
（1）证明：△ABO≌△CAE，并求点C的坐标．
（2）在坐标平面内是否存在一点P（不与点C重合），使△PAB与△ABC全等？若存在，求出点P的坐标；若不存在，请说明理由．
【考点】几何变换综合题．
【答案】（1）证明过程见解答，点C的坐标为（-5，7）；
（2）点P的坐标为（5，3）或（-7，2）或（3，-2）．
（2）点P的坐标为（5，3）或（-7，2）或（3，-2）．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/9/7 12:0:8组卷：314引用：1难度：0.1
相似题
-
1．如图1，把等腰直角三角板AMN放在平面直角坐标系xOy中，点A坐标为（0，4），∠MAN=90°，AM=AN．三角板AMN绕点A逆时针旋转，AM、AN与x轴分别交于点D、E，∠AOE、∠AOD的角平分线OG、OH分别交AN、AM于点B、C．点P为BC的中点．
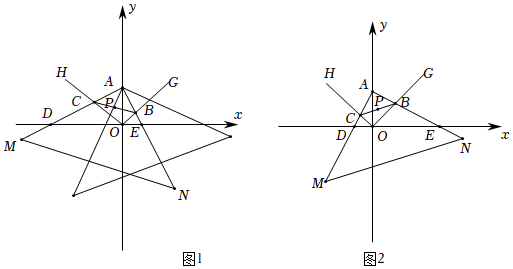
（1）求证：AB=AC；
（2）如图2，若点D的坐标为（-3，0），求线段BC的长度；
（3）在旋转过程中，若点D的坐标从（-8，0）变化到（-2，0），则点P的运动路径长为
（直接写出结果）．发布：2025/5/25 19:0:2组卷：72引用：1难度：0.2 -
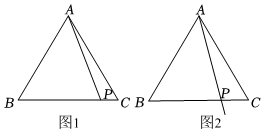2．如图1，等边△ABC中，点P是BC边上一点，作点C关于直线AP的对称点D，连接CD，BD，作AE⊥BD于点E；
（1）若∠PAC=10°，依题意补全图1，并直接写出∠BCD的度数；
（2）如图2，若∠PAC=α（0°＜α＜30°），
①求证：∠BCD=∠BAE；
②用等式表示线段BD，CD，AE之间的数量关系 ．发布：2025/5/25 19:30:2组卷：186引用：2难度：0.3 -
3．[问题发现]如图1，在Rt△ABC中，∠BAC=90°，AB=AC，D为斜边BC上一点（不与点B，C重合），将线段AD绕点A顺时针旋转90°得到AE，连接EC，则线段BD与CE的数量关系是 ，位置关系是 ；
[探究证明]如图2，在Rt△ABC和Rt△ADE中，∠BAC=∠DAE=90°，AB=AC．AD=AE，将△ADE绕点A旋转，当点C，D，E在同一条直线上时，BD与CE具有怎样的位置关系，说明理由；
[拓展延伸]如图3，在Rt△BCD中，∠BCD=90°，BC=2CD=4，过点C作CA⊥BD于A．将△ACD绕点A顺时针旋转，点C的对应点为点E．设旋转角∠CAE为a（0°＜a＜360°），当C，D，E在同一条直线上时，画出图形，并求出线段BE的长度．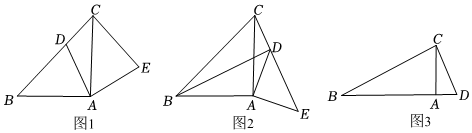
发布：2025/5/25 22:0:1组卷：405引用：1难度：0.3
