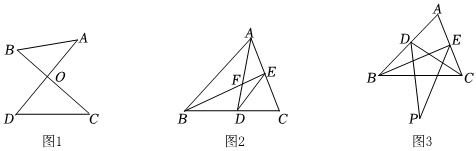
我们将内角互为对顶角的两个三角形称为“对顶三角形”．例如，在图1中，△AOB的内角∠AOB与△COD的内角∠COD为对顶角，则△AOB与△COD为“对顶三角形”，根据三角形三个内角和是180°，“对顶三角形”有如下性质：∠A+∠B=∠C+∠D．

性质理解：
（1）如图1，在“对顶三角形”△AOB与△COD中，则∠AOB=85°，则∠C+∠D=

95

95

°．
性质应用：
（2）如图2，在△ABC中，AD、BE分别平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大8°，求∠BED的度数．
拓展提高：
（3）如图3，BE、CD是△ABC的角平分线，且∠BDC和∠BEC的平分线DP和EP相交于点P，设∠A=α，请尝试求出∠P的度数（用含α的式子表示∠P）．