综合与实践
问题情境
在学习了《勾股定理》和《实数》后，某班同学以“已知三角形三边的长度，求三角形面积”为主题开展了数学活动．
操作发现
“毕达哥拉斯”小组的同学想到借助正方形网格解决问题．如图1是6×6的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点称为格点．在图1中画出△ABC，其顶点A，B，C都是格点，同时构造正方形BDEF，使它的顶点都在格点上，且它的边DE，EF分别经过点C、A，他们借助此图求出了△ABC的面积．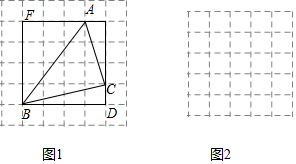
（1）在图1中，所画的△ABC的三边长分别是AB=

5

5

，BC=

17

17

，AC=

10

10

；△ABC的面积为

13

2

13

2

．
实践探究
（2）在图2所示的正方形网格中画出△DEF（顶点都在格点上），使DE=

5

，DF=

13

，EF=

20

，并写出△DEF的面积．
继续探究
“秦九韶”小组的同学想到借助曾经阅读的数学资料：
已知三角形的三边长分别为a、b、c,求其面积，对此问题中外数学家曾经进行过深入研究．古希腊的几何学家海伦（Heron,约公元50年），在他的著作《度量》一书中，给出了求其面积的海伦公式

S

=

p

（

p

-

a

）

（

p

-

b

）

（

p

-

c

）

其中

p

=

a

+

b

+

c

2

①

我国南宋时期数学家秦九韶（约1202～1261），给出了著名的秦九韶公式

S

=

1

4

[

a

2

b

2

-

（

a

2

+

b

2

-

c

2

2

）

2

]

．

②

（3）一个三角形的三边长依次为

5

，

6

，

7

，请你从上述材料中选用适当的公式求这个三角形的面积．（写出计算过程）