课本再现
（1）如图1，△ABD，△AEC都是等边三角形．BE与CD有什么关系？你能用旋转的性质说明上述关系成立的理由吗？
探究应用
（2）如图2，△ADC绕着点A逆时针旋转90°得到△ABE，连接CE，BD，BC，DE．
①下列说法正确的是 A，B，DA，B，D；（填序号，错选不得分）
A．△AEC，△ABD的形状都是等腰直角三角形
B．CD=BE，CD⊥BE
C．S四边边形BCED=BE2
D．△ABC的面积与△AED的面积相等
②如图3，点M是BC的中点，判断AM与DE之间的关系，并证明．
（3）在（1）中，若BC=6，DC与BE交于点H，过点C向上作线段CG⊥BC于点C，CG=23，连接GH．请直接写出GH的最小值．
3
【考点】四边形综合题．
【答案】A，B，D
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/10/6 5:0:1组卷：157引用：1难度：0.1
相似题
-
1．在平行四边形ABCD中，M，N分别是边AD，AB的点，AB=kAN，AD=kAM．
（1）如图1，若连接MN，BD，求证：MN∥BD；
（2）如图2，把△AMN绕点A顺时针旋转角度α（0°＜α＜90°）得到△AFE，M，N的对应点分别为点E，F，连接BE，若∠ABF=∠EBC，∠AEB=2∠DAE．
①直接写出k的取值范围；
②当tan∠EBC=时，求k的值．13
发布：2025/5/26 11:30:1组卷：207引用：3难度：0.2 -
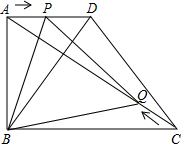2．如图，在四边形ABCD中，AD∥BC，∠DAB=90°，AB=6cm,BC=8cm,AD=4cm.点P从点A出发沿AD向点D匀速运动，速度是1cm/s；同时，点Q从点C出发沿CA 向点A匀速运动，速度是1cm/s,当一个点到达终点，另一个点立即停止运动．连接PQ，BP，BQ，设运动时间为t（s），解答下列问题：
（1）当t为何值时，PQ∥CD？
（2）设△BPQ的面积为s（cm2），求s与t之间的函数关系式；
（3）是否存在某一时刻t,使得△BPQ的面积为四边形ABCD面积的？若存在，求出此时t的值；若不存在，说明理由；12
（4）连接BD，是否存在某一时刻t,使得BP平分∠ABD？若存在，求出此时t的值；若不存在，说明理由．发布：2025/5/26 12:0:1组卷：399引用：2难度：0.1 -
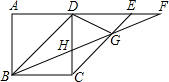3．如图，正方形ABCD中，在AD的延长线上取点E，F，使DE=AD，DF=BD，连接BF分别交CD，CE于H，G下列结论正确的有．（填序号）
①GD=GH；②EC=2DG；③S△CDG=S四边形DHGE； ④图中有7个等腰三角形．发布：2025/5/27 4:0:1组卷：172引用：1难度：0.5
