阅读下列材料：
小明遇到这样一个问题：在△ABC中AB，BC，AC分别为2，5，5．求△ABC的面积
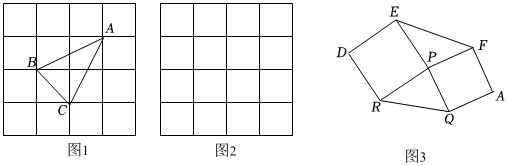
小明是这样解决问题的：如图1所示．先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点三角形ABC（即△ABC三个顶点都在小正方形的顶点处），借助网格就能计算出△ABC的面积．他把这种解决问题的方法称为构图法．
请回答：
（1）图1中△ABC的面积为 1.51.5．
参考小明解决问题的方法，完成下列问题：
（2）如图2所示为一个4×4的正方形网格（每个小正方形的边长为1）．
①利用构图法在图2中画出三边长分别为2，13，17的格点△DEF．
②△DEF的面积为 2.52.5．
（3）如图3所示，已知△PQR，分别以PQ，PR为边向外作正方形PQAF，正方形PRDE，连接EF．若PQ2=5，PR2=10，QR2=13，求六边形AQRDEF的面积．
2
5
5
2
13
17
【答案】1.5；2.5
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/29 5:0:9组卷：33引用：1难度：0.5
相似题
-
1．将如图所示的四个正方形分别分割成可以剪下4个、7个、8个和9个正方形的图形．
发布：2025/6/17 17:30:2组卷：63引用：1难度：0.7 -
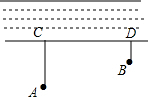2．如图所示，牧童在A处放羊，其家在B处，A，B到河岸的距离分别为AC=400m,BD=200m,C、D间的距离为800m,牧童从A处把羊牵到河近饮水后再回家，试问：羊在何处饮水所走路程最短？在图中画出最短路径并求出最短路径的长度是多少．发布：2025/6/17 23:0:1组卷：283引用：2难度：0.4 -
3．将正方形ABCD（如图1）作如下划分：
第1次划分：分别连接正方形ABCD对边的中点（如图2），得线段HF和EG，它们交于点M，此时图2中共有5个正方形；
第2次划分：将图2左上角正方形AEMH再作划分，得图3，则图3中共有9个正方形；
（1）若每次都把左上角的正方形一次划分下去，则第100次划分后，图中共有个正方形；
（2）继续划分下去，第几次划分后能有805个正方形？写出计算过程．
（3）能否将正方形ABCD划分成有2015个正方形的图形？如果能，请算出是第几次划分，如果不能，需说明理由．
（4）如果设原正方形的边长为1，通过不断地分割该面积为1的正方形，并把数量关系和几何图形巧妙地结合起来，可以很容易得到一些计算结果，试着探究求出下面表达式的结果吧．
计算（1+34+14+142+…+143）．（直接写出答案即可）14n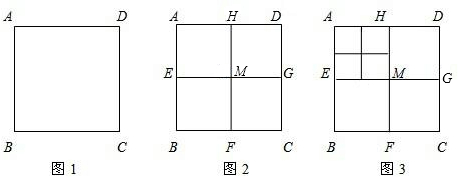
发布：2025/6/18 3:30:2组卷：274引用：4难度：0.3
