顶点为D的抛物线y=-x2+bx+c交x轴于A、B（3，0），交y轴于点C，直线y=-34x+m经过点C，交x轴于E（4，0）．
（1）求出抛物线的解析式；
（2）如图1，点M为线段BD上不与B、D重合的一个动点，过点M作x轴的垂线，垂足为N，设点M的横坐标为x,四边形OCMN的面积为S，求S与x之间的函数关系式，并求S的最大值；
（3）点P为x轴的正半轴上一个动点，过P作x轴的垂线，交直线y=-34x+m于G，交抛物线于H，连接CH，将△CGH沿CH翻折，若点G的对应点F恰好落在y轴上时，请直接写出点P的坐标．
3
4
3
4
【考点】二次函数综合题．
【答案】见试题解答内容
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/22 8:0:1组卷：622引用：5难度：0.2
相似题
-
1．抛物线与坐标轴交于A（-1，0），B（4，0），C（0，2）．
（1）求抛物线的解析式；
（2）点D是x轴上的一点，过点D作EF∥AC，交抛物线于E、F，当EF=3AC时，求出点D的坐标；
（3）点D是x轴上的一点，过点D作DE∥AC，交线段BC于E，将△DEB沿DE翻折，得到△DEB′，若△DEB′与△ABC重合部分的面积为S，点D的横坐标为m,直接写出S与m的函数关系式并写出取值范围．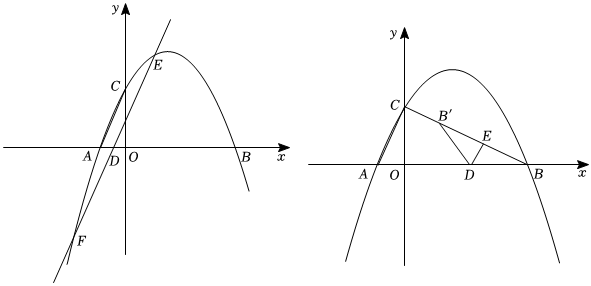
发布：2025/5/24 4:0:7组卷：188引用：1难度：0.1 -
2．如图，在平面直角坐标系xOy中，正比例函数y=kx（k≠0）和二次函数y=-
x2+bx+3的图象都经过点A（4，3）和点B，过点A作OA的垂线交x轴于点C．D是线段AB上一点（点D与点A、O、B不重合），E是射线AC上一点，且AE=OD，连接DE，过点D作x轴的垂线交抛物线于点F，以DE、DF为邻边作▱DEGF．14
（1）填空：k=，b=；
（2）设点D的横坐标是t（t＞0），连接EF．若∠FGE=∠DFE，求t的值；
（3）过点F作AB的垂线交线段DE于点P，若S△DFP=S▱DEGF，求OD的长．13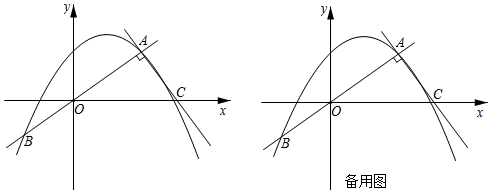
发布：2025/5/24 4:0:7组卷：3463引用：4难度：0.1 -
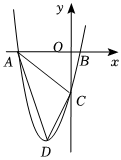3．如图，抛物线y=x2+4x-5与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C，抛物线的顶点为D．
（1）求△ACD的面积；
（2）在y轴上是否存在点E，使△ADE是直角三角形？若存在，请求出点E的坐标；若不存在，请说明理由．发布：2025/5/24 4:0:7组卷：41引用：1难度：0.3
