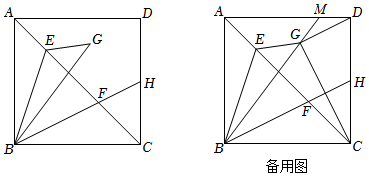
如图，正方形ABCD，点E，F是对角线AC上的两个动点，连接BE，BF，延长BF交CD于点H，∠EBF=45°．△ABE和△GBE关于直线BE对称．
（1）求证：∠FBG=∠FBC；
（2）如备用图，若点H是CD边的中点，连接DG，CG．延长BG交AD于点M．
①求证：DG⊥CG；②求MDAD的值．
MD
AD
【考点】四边形综合题．
【答案】（1）（2）①证明见解答；②．
1
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/13 8:0:9组卷：313引用：3难度：0.4
相似题
-
1．如图，边长一定的正方形ABCD，Q为CD上一个动点，AQ交BD于点M，过M作MN⊥AQ交BC于点N，作NP⊥BD于点P，连接NQ，下列结论：①AM=MN；②MP=BD；③BN+DQ=NQ；④12为定值．其中一定成立的是 ．AB+BNBM发布：2025/6/24 15:0:1组卷：2074引用：8难度：0.5 -
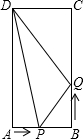2．如图，在矩形ABCD中，AB=6cm,BC=12cm,点P沿边AB从点A向点B以1cm/s的速度移动；同时，点Q从点B沿边BC向点C以2cm/s的速度移动，设点P、Q移动的时间为t s.问：
（1）当t为何值时△PBQ的面积等于8cm2？
（2）当t为何值时△DPQ是直角三角形？
（3）是否存在t的值，使△DPQ的面积最小，若存在，求此时t的值及此时的面积；若不存在，请说明理由．发布：2025/6/23 18:0:2组卷：117引用：1难度：0.1 -
3．已知菱形ABCD的边长为1，∠ADC=60°，等边△AEF两边分别交DC、CB于点E、F．
（1）特殊发现：如图1，若点E、F分别是边DC、CB的中点，求证：菱形ABCD对角线AC、BD的交点O即为等边△AEF的外心；
（2）若点E、F始终分别在边DC、CB上移动，记等边△AEF的外心为P． ①猜想验证：如图2，猜想△AEF的外心P落在哪一直线上，并加以证明；②拓展运用：如图3，当E、F分别是边DC、CB的中点时，过点P任作一直线，分别交DA边于点M，BC边于点G，DC边的延长线于点N，请你直接写出的值．1DM+1DN
发布：2025/6/23 21:30:2组卷：421引用：6难度：0.5
