【情景引入】:
(1)如图1,BD、CD分别是△ABC的内角∠ABC、∠ACB的平分线,说明∠D=90°+12∠A的理由.
【深入探究】:
(2)①如图2,BD、CD分别是△ABC的两个外角∠EBC、∠FCB的平分线,∠D与∠A之间的等量关系是 ∠D=90°-12∠A∠D=90°-12∠A;
②如图3,BD、CD分别是△ABC的一个内角∠ABC和一个外角∠ACE的平分线,∠D与∠A之间的等量关系是 ∠D=12∠A∠D=12∠A.
【拓展应用】:
(3)请用以上结论解决下列问题:如图4,在△ABC中,BD、CD分别平分∠ABC、∠ACB,M、N、Q分别在DB、DC、BC的延长线上,BE、CE分别平分∠MBC、∠BCN,BF、CF分别平分∠EBC、∠ECQ.
①∠A=80°,则∠F的度数为 12.5°12.5°;
②∠F=n°,则∠A的度数为 180°-8n°180°-8n°.

∠
D
=
90
°
+
1
2
∠
A
1
2
1
2
1
2
1
2
【答案】∠D=90°-∠A;∠D=∠A;12.5°;180°-8n°
1
2
1
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/5/25 8:0:9组卷:833引用:1难度:0.3
相似题
-
1.下面是投影屏上出示的抢答题,需要回答横线上符号代表的内容,则回答正确的是( )
已知:如图,∠BEC=∠B+∠C.
求证:AB∥CD.
证明:延长BE交※于点F,则
∠BEC=⊙+∠C(三角形的外角等于与它不相邻两个内角之和).
又∠BEC=∠B+∠C,得∠B=▲
故AB∥CD(@相等,两直线平行) 发布:2025/5/22 1:0:1组卷:225引用:5难度:0.6
发布:2025/5/22 1:0:1组卷:225引用:5难度:0.6 -
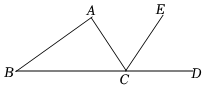 2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=65°,则∠A的度数为( )发布:2025/5/21 23:0:1组卷:102引用:3难度:0.7
2.如图,CE是△ABC的外角∠ACD的平分线,若∠B=40°,∠ACE=65°,则∠A的度数为( )发布:2025/5/21 23:0:1组卷:102引用:3难度:0.7 -
 3.已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
3.已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:
(1)∠BDC的度数;
(2)∠BFD的度数.发布:2025/1/23 8:0:2组卷:1121引用:9难度:0.5


