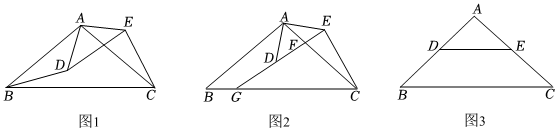
【阅读材料】两个顶角相等的等腰三角形，若它们的顶角具有公共的顶点，且当把它们底角的顶点连接起来时会形成一组全等三角形，则把具有这种规律的图形称为“手拉手”图形．如图1，在“手拉手”图形中，若∠BAC=∠DAE，AB=AC，AD=AE，则△ABD≌△ACE．
【材料理解】在图1中证明△ABD≌△ACE．
【问题解决】如图2，△ABC和△ADE都是等腰三角形，∠BAC=∠DAE，AB=AC，AD=AE，线段DE与线段AC交于点F，延长ED交BC于点G，求证：∠BAD=∠CGE．下面是小明的部分证明过程：
证明：∵AB=AC，AD=AE，
∴∠ABC=∠ACB=12（180°-∠BAC），∠AED=∠ADE=12（180°-∠DAE），
∵∠BAC=∠DAE，
∴∠ACB=∠AED．
请你补全余下的证明过程．
【结论应用】如图3，△ABC是等腰三角形，∠BAC=100°，D、E分别为边AB、AC上的点，且满足AD=AE，连结DE，将△ADE以点A为旋转中心按逆时针方向旋转，旋转角为α（0°＜α＜360°），当线段DE与△ABC的腰有交点，且直线DE垂直于△ABC的腰时，直接写出α的值．
1
2
1
2
【考点】几何变换综合题．
【答案】（1）见解答部分；
（2）见解答部分；
（3）符合题意的α的值为50°或310°．
（2）见解答部分；
（3）符合题意的α的值为50°或310°．
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/7/21 8:0:9组卷：515引用：1难度：0.2
相似题
-
1．如图1，点D是等边△ABC外一点，且满足CD=BD，∠BDC=120°．
（1）如图2，将△BDC绕点B顺时针旋转30°得到△BDE，连接AD、CE．若AC=3，求△ABD的面积；
（2）如图3，将△BDC绕点B顺时针旋转α（α＜90°）得到△BDE，取CE的中点F，连接DF，求证：AD=2DF；
（3）如图4，将△BDC绕点B顺时针旋转α得到△BDE，延长BC至点H，使得CH=BC，连接AH，EH，M、N分别为HE、BE的中点，连接AN、AM、MN．若BC=3，当AM最大时，直接写出△AMN的周长．13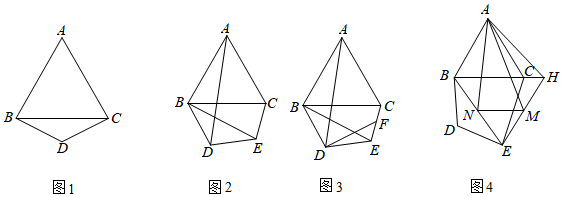
发布：2025/6/21 21:30:1组卷：138引用：1难度：0.1 -
2．如图1，在等边△ABC中，点E是边AC上一点，连接BE，作CF⊥BE于点F，将线段CF绕点C顺时针旋转60°得到线段CD，连接AD．
（1）如图1，已知AB=4，AE=1，求线段CF的长；
（2）如图2，连接DF，并延长DF交AB于点H，求证：AH=BH；
（3）若BC=4，点E为线段AC上一动点，当线段AF的长最小时，求△AFD的面积．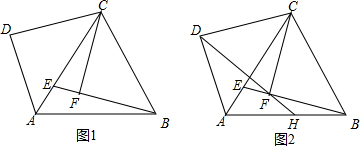
发布：2025/6/21 19:30:1组卷：175引用：1难度：0.1 -
3．在△ABC和△ADE中，∠BAC=∠ADE=90°，AB=AC，DE=DA．且AC＞AD．
（1）如图1，点D在线段AC上时，连接BE，若AC=4，AE=6，求线段EB的长；2
（2）如图2，将图1中△ADE绕着点A逆时针旋转，使点D在△ABC的内部，连接BD，CD．线段AE，BD相交于点F，过点A作AH⊥BC交BC于点H，当∠DCB=∠DAC时，求证：BF=DF；
（3）如图3，点C'是点C关于AB的对称点，连接C′A，C′B．在（2）的基础上继续逆时针旋转△ADE，过B作AD的平行线，交直线EA于点G．连接C′G，CG，BD．若BC=4，当线段C′G最短时，直接写出△ACG的面积．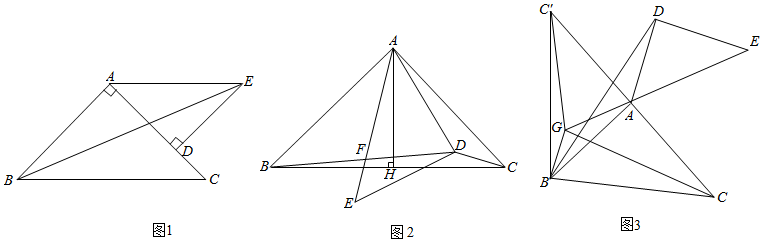
发布：2025/6/21 19:30:1组卷：388引用：1难度：0.2
