【概念学习】规定:求若干个相同的有理数(均不等0)的除法运算叫做除方,如2÷2÷2,类比有理数的乘方,把2÷2÷2记作2③,读作“2的圈3次方”.一般地,把a÷a÷a÷…÷an个(a≠0)记作a⑪,读作“a的圈n次方”.
【初步探究】
(1)直接写出计算结果:2③=1212;
【深入思考】我们知道,有理数的除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?

(2)仿照上面的算式,将运算结果直接写成幂的形式:3④=(13)2(13)2;
(3)将一个非零有理数a的圈n次方写成幂的形式是 (1a)n-2(1a)n-2;
(4)计算:62÷(-13)④×(-2)③.
【拓展延伸】
为解决上面的数学问题,我们可以运用数形结合的思想方法,通过不断地分割一个面积为1的正方形,把数量关系和几何图形巧妙地结合起来.
如计算12+122+123+…+12n.
第1次分割,把正方形的面积二等分,其中阴影部分的面积为12;
第2次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为12+122;
第3次分割,把上次分割图中空白部分的面积继续二等分,阴影部分的面积之和为12+122+123;
…
第n次分割,把上次分割图中空白部分的面积最后二等分,所有阴影部分的面积之和为12+122+123+…+12n,最后空白部分的面积是12n.
根据第n次分割图可得等式:12+122+123+…+12n=1-12n.

(5)求3③+3④+3⑤+…+3(2021)的值,请你在面积为1的正方形(备用图)上画出分割图,并在图上标注阴影部分面积.
a
÷
a
÷
a
÷
…
÷
a
n
个
1
2
1
2
(
1
3
)
2
(
1
3
)
2
(
1
a
)
n
-
2
(
1
a
)
n
-
2
6
2
÷
(
-
1
3
)
④
×
(
-
2
)
③
1
2
+
1
2
2
+
1
2
3
+
…
+
1
2
n
1
2
1
2
+
1
2
2
1
2
+
1
2
2
+
1
2
3
1
2
+
1
2
2
+
1
2
3
+
…
+
1
2
n
1
2
n
1
2
+
1
2
2
+
1
2
3
+
…
+
1
2
n
1
-
1
2
n
【考点】规律型:图形的变化类;有理数的混合运算.
【答案】;;
1
2
(
1
3
)
2
(
1
a
)
n
-
2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/9/16 11:0:11组卷:175引用:3难度:0.4
相似题
-
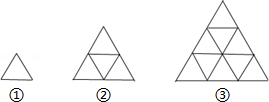
1.下列是用火柴棒拼成的一组图形,第①个图形中有3根火柴棒,第②个图形中有9根火柴棒,第③个图形中有18根火柴棒,…依此类推,则第6个图形中火柴棒根数是( )
 发布:2025/6/14 2:30:1组卷:154引用:4难度:0.7
发布:2025/6/14 2:30:1组卷:154引用:4难度:0.7 -
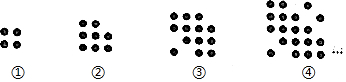
2.下列图形都是由●按照一定规律组成的,其中第①个图中共有4个●,第②个图中共有8个●,第③个图中共有13个●,第④个图中共有19个●,…,照此规律排列下去,则第⑨个图中●的个数为( )
 发布:2025/6/14 4:0:2组卷:500引用:11难度:0.7
发布:2025/6/14 4:0:2组卷:500引用:11难度:0.7 -
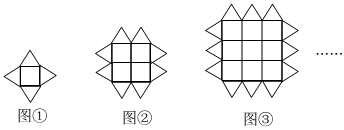
3.下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中一共有5个正多边形,第②个图形中一共有13个正多边形,第③个图形中一共有26个正多边形,则第⑤个图形中正多边形的个数为( )
 发布:2025/6/14 1:0:2组卷:95引用:7难度:0.7
发布:2025/6/14 1:0:2组卷:95引用:7难度:0.7


