对于平面直角坐标系xOy中的点C及图形W,有如下定义:若图形W上存在A、B两点,使△ABC为等腰直角三角形,且∠ABC=90°,我们则称点C为图形W的“关联点”.
(1)已知点O(0,0),M(4,0),在点C1(0,4),C2(2,1),C3(3,-4)中,线段OM的“关联点”是 C1,C2C1,C2;
(2)直线y=x+b分别交x轴、y轴于P、Q两点,若点C(-2,1)为线段PQ的“关联点”,求b的取值范围;
(3)已知直线y=-x+m(m>0)分别交x轴、y轴于E、F两点,若线段EF上的所有点都是半径为1的⊙O的“关联点”,直接写出m的取值范围.
【考点】圆的综合题.
【答案】C1,C2
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/10/22 11:0:1组卷:31引用:2难度:0.5
相似题
-
1.如图,直线y=2交y轴于点A,点B(m,2)(其中m>0)在直线y=2上运动.以线段AB为斜边向下作Rt△ABC.
(1)若m=5,且点C恰好落在x轴上,则点C的坐标为 ;
(2)若有且仅有一个点C恰好落在x轴上.
①此时m的值为 ;
②如图2,以AB为直径作半圆,将线段AB绕点A顺时针旋转,使点B落在x轴正半轴上,则半圆里未被线段AB扫过的部分(即弓形AMH)面积为 ;
(3)若点C不会落在x轴上,则m的取值范围为 .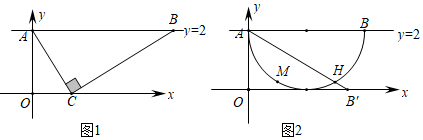 发布:2025/6/17 6:30:2组卷:73引用:1难度:0.3
发布:2025/6/17 6:30:2组卷:73引用:1难度:0.3 -
 2.对于坐标系中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,能使得∠APB=60°,则称点P为⊙C的关联点.
2.对于坐标系中的点P和⊙C,给出如下定义:若⊙C上存在两个点A,B,能使得∠APB=60°,则称点P为⊙C的关联点.
如图,已知点P(0.5,0)、Q(1,0)、M(2,0)、N(3,0).
(1)若⊙O的半径为1,点A,B在⊙O上运动.
①∠AMB的最大值为 °;
②在点P、Q、M、N中,是⊙O关联点的有 ;
③⊙O所有关联点形成的区域面积为 ;
④过点M与G(0,)作直线l,直线l上的点H(m,n)是⊙O的关联点,求m的取值范围;23
(2)若要使上题中,线段MG上所有点都是⊙O的关联点,则⊙O半径应该扩大,请求出⊙O半径r的最小值.发布:2025/6/17 6:30:2组卷:94引用:1难度:0.3 -
3.如图1,已知点A(6,0),B(0,6),点C在半径为3的⊙O上运动,将OC顺时针旋转90°得到OD.
(1)当OC∥AB时,则∠BOC=°;
(2)如图2,若点E在线段AB上运动,连接DE,AC,BC.
①线段DE长度的最小值是 ;
②△ABC的面积最大值是 .
(3)如图3,连接AD,BC.
①当OC∥AD时,求证:BC是⊙O的切线;
②在整个运动过程中,若直线AD,BC交于点P,则下列命题错误的是 .
A.线段AD,BC的关系为互相垂直且相等
B.点P的纵坐标的最小值为3-32
C.点P的纵坐标的最大值为3+32
D.点P的运动轨迹为圆弧,该圆弧长为2π2 发布:2025/6/17 6:30:2组卷:90引用:1难度:0.1
发布:2025/6/17 6:30:2组卷:90引用:1难度:0.1


