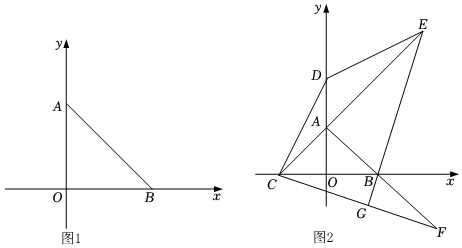
如图1，在平面直角坐标系中，点A在y轴上，点B在x轴上，∠ABO=45°，且A（0，3）．
（1）直接写出B点坐标；
（2）动点P从点O出发，以每秒钟2个单位长度的速度沿x轴的正方向运动，连接AP，设△ABP的面积为S，若点P运动的时间为t秒，请用含t的代数式表示S，并直接写出t的取值范围；
（3）在（2）的条件下，如图2，点E（15-3mm+1，9m）在第一象限，射线EA交x轴于点C，线段CE的垂直平分线交y轴于点D，过C点作CG⊥BE于点G，交AB的延长线于点F，当∠ADE-∠CDO=90°，且满足S=94时，求△DPF的面积？
15
-
3
m
m
+
1
9
m
9
4
【考点】三角形综合题．
【答案】（1）（3，0）．
（2）当0≤t≤时，S△ABP=；当t≥时，S△ABP=3t-．
（3）或．
（2）当0≤t≤
3
2
9
2
-
3
t
3
2
9
2
（3）
45
4
9
4
【解答】
【点评】
声明：本试题解析著作权属菁优网所有，未经书面同意，不得复制发布。
发布：2024/8/14 1:0:1组卷：35引用：3难度：0.5
相似题
-
1．在平面直角坐标系中，点A、B、C的坐标分别为（m,0），（2，-4），（n,0），且m,n满足方程（m-2）xn-4+
=0为二元一次方程．ym2-3
（1）求A、C的坐标；
（2）若点D为y轴正半轴上的一个动点．
①如图1，已知∠DAO=∠ACB，∠ADO与∠ACB的角平分线交于点P，求∠P的度数；
②如图2，连接BD，交x轴于点E．若S△ADE≤S△BCE成立．设动点D坐标为（0，a），求a的取值范围．
发布：2025/6/8 0:30:1组卷：83引用：1难度：0.1 -
2．在平面直角坐标系中，A（a,0），C（b,2），且满足（a+b）2+|a-b+4|=0，过C作CB⊥x轴于B．
（1）如图1，求△ABC的面积．
（2）如图2，若过B作BD∥AC交y轴于D，在△ABC内有一点E，连接AE、DE，若∠CAE+∠BDE=∠EAO+∠EDO，求∠AED的度数．
（3）如图3，在（2）的条件下，DE与x轴交于点M，AC与y轴交于点F，作△AME的角平分线MP，在PE上有一点Q，连接QM，∠EAM+2∠PMQ=45°，当AE=mAM，FO=2QM时，求点E的纵坐标（用含m的代数式表示）．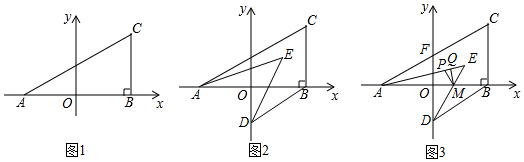
发布：2025/6/7 23:0:2组卷：189引用：2难度：0.2 -
3．如图，在平面直角坐标系xOy中，已知A（a,0），B（b,m），且满足（a-6）2+
=0，m是36的算术平方根，将线段OA平移至CB，点D在x轴正半轴上（不与点A重合），连接OC，AB，CD，BD．b-8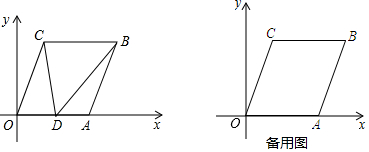
（1）直接写出点A、B、C的坐标；
（2）当△ODC的面积是△ABD的面积的3倍时，求点D的坐标；
（3）已知OC∥AB，设∠OCD=α，∠DBA=∠β，∠BDC=θ，判断α、β、θ之间的数量关系，并说明理由．发布：2025/6/7 21:30:1组卷：284引用：4难度：0.4
