乘法公式的探究及应用.
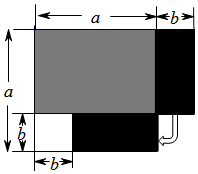
(1):如图1,可以求出阴影部分的面积是a2-b2a2-b2(写成两数平方差的形式);
(2):如图2,若将阴影部分裁剪下来,重新拼成一个矩形,它的宽是a-ba-b,长是a+ba+b,面积是(a+b)(a-b)(a+b)(a-b).(写成多项式乘法的形式)
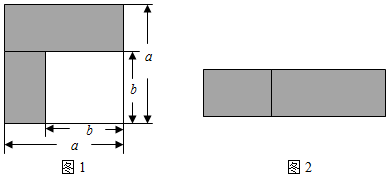
(3):比较图1,图2的阴影部分面积,可以得到乘法公式a2-b2=(a+b)(a-b)a2-b2=(a+b)(a-b)(用式子表达)
(4):应用所得的公式计算:(1-122)(1-132)(1-142)…(1-1992)(1-11002)
1
2
2
1
3
2
1
4
2
1
99
2
1
100
2
【考点】平方差公式的几何背景;完全平方公式的几何背景.
【答案】a2-b2;a-b;a+b;(a+b)(a-b);a2-b2=(a+b)(a-b)
【解答】
【点评】
声明:本试题解析著作权属菁优网所有,未经书面同意,不得复制发布。
发布:2024/8/12 8:0:1组卷:942引用:3难度:0.8